
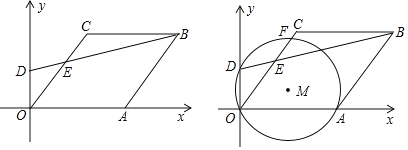
°æƒø°ø»ÁÕº£¨“—÷™∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨µ„C£®3£¨4£©£¨“‘OCŒ™±þ◊˜¡‚–ŒOABC£¨«“µ„A¬‰‘⁄x÷·µƒ’˝∞Î÷·…œ£¨µ„DŒ™y÷·…œµƒ“ª∏ˆ∂ص„£¨…ËD£®0£¨m£©£¨¡¨Ω·DB£¨Ωª÷±œþOC”⁄µ„E£Æ
£®1£©ÃÓø’£∫Bµƒ◊¯±ÍŒ™£®°° °°£©£¨sin°œAOC£Ω°° °°£ª
£®2£©µ±µ„D‘⁄y÷·’˝∞Î÷· ±£¨º«°˜DEOµƒ√ʪ˝Œ™S1£¨°˜BCEµƒ√ʪ˝Œ™S2£¨µ±S1£ΩS2 ±£¨«Ûmµƒ÷µ£Æ
£®3£©π˝µ„D£¨O£¨A◊˜°—M£¨Ωªœþ∂ŒOC”⁄µ„F£Æ
¢Ÿµ±°—M”Ρ‚–ŒOABC“ª±þÀ˘‘⁄µƒ÷±œþœý«– ±£¨«ÛÀ˘”–¬˙◊„Ãıº˛µƒmµƒ÷µ£Æ
¢⁄µ±OD£ΩDE ±£¨÷±Ω”–¥≥ˆOE:EFµƒ÷µ£Æ
°æ¥∞∏°ø£®1£©£®8£¨4£©£¨![]() £ª£®2£©m£Ω
£ª£®2£©m£Ω![]() £ª£®3£©¢Ÿ¬˙◊„Ãıº˛µƒmµƒ÷µŒ™
£ª£®3£©¢Ÿ¬˙◊„Ãıº˛µƒmµƒ÷µŒ™![]() ªÚ
ªÚ![]() £ª¢⁄OE:EFµƒ÷µ8:5£Æ
£ª¢⁄OE:EFµƒ÷µ8:5£Æ
°æΩ‚Œˆ°ø
£®1£©»ÁÕº1÷–£¨◊˜CH°ÕOA”⁄H£Æ∏˘æðµ„Cµƒ◊¯±Í«Û≥ˆOH£¨CH ¿˚”√π¥π…∂®¿Ì«Û≥ˆOCº¥ø…Ω‚æˆŒ £ª
£®2£©»ÁÕº1÷–£¨—”≥§BCΩªOD”⁄F£Æ”…S1=S2£¨Õ∆≥ˆS°˜OCF=S°˜BDF£¨”…¥ÀππΩ®∑Ω≥ú¥ø…Ω‚æˆŒ £ª
£®3£©¢Ÿ∑÷¡Ω÷÷«È–Œ£∫»ÁÕº2÷–£¨µ±°—M”ÎBCœý«– ±£¨∏˘æðPQ=DM£¨ππΩ®∑Ω≥ú¥ø…Ω‚æˆŒ £ƻÁÕº3÷–£¨µ±°—M”ÎABœý«– ±£¨AD°ÕAB£¨…ËADΩªOC”⁄Q£Æ∏˘æðtam°œOAD=tan°œDOC=![]() £¨ππΩ®∑Ω≥ú¥ø…Ω‚æˆŒ £ª
£¨ππΩ®∑Ω≥ú¥ø…Ω‚æˆŒ £ª
¢⁄»ÁÕº4÷–£¨◊˜BG°ÕBCΩªOCµƒ—”≥§œþ”⁄G£¨¡¨Ω”DF£¨AF£¨◊˜FP°ÕOA”⁄P£Æ ◊œ»«Û≥ˆBG£¨‘Ÿ÷§√˜BE=BG£¨∏˘æðDE+BE=BD£¨ππΩ®∑Ω≥ëÛ≥ˆm£¨…ËOF=5k£¨‘ÚFP=4k£¨OP=3k£¨‘⁄Rt°˜APF÷–£¨∏˘æðAF2=PF2+PA2£¨ππΩ®∑Ω≥ëÛ≥ˆkº¥ø…Ω‚æˆŒ £Æ
£®1£©»ÁÕº1÷–£¨◊˜CH°ÕOA”⁄H£Æ
°þC(3£¨4)£¨CH°ÕOA£¨
°ýOH£Ω3£¨CH£Ω4£¨
°ýOC£Ω![]() £Ω
£Ω![]() £Ω5£¨
£Ω5£¨
°þÀƒ±þ–ŒABCD «¡‚–Œ£¨
°ýOA£ΩAB£ΩOC£ΩBC£Ω5£¨BC°ŒOA£¨
°ýB(8£¨4)£¨
°ýsin°œAOC£Ω![]() £Ω
£Ω![]() £Æ
£Æ
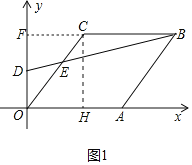
£®2£©»ÁÕº1÷–£¨—”≥§BCΩªOD”⁄F£Æ
°þS1£ΩS2£¨
°ýS°˜OCF£ΩS°˜BDF£¨
°ý![]() °¡3°¡4£Ω
°¡3°¡4£Ω![]() °¡(4©Åm)°¡8£¨
°¡(4©Åm)°¡8£¨
Ω‚µ√m£Ω![]() £Æ
£Æ
£®3£©¢Ÿ»ÁÕº2÷–£¨—”≥§BCΩªOD”⁄P£¨◊˜MQ°ÕOD”⁄Q£Æ
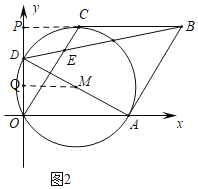
µ±°—M”ÎBCœý«– ±£¨PQ£ΩDM£Æ
‘Ú”–4©Å![]() £Ω
£Ω![]()
![]() £¨
£¨
Ω‚µ√m£Ω![]() £Æ
£Æ
»ÁÕº3÷–£¨µ±°—M”ÎABœý«– ±£¨AD°ÕAB£¨…ËADΩªOC”⁄Q£Æ
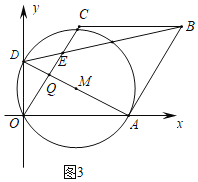
°þOC//AB£¨
°ýOC°ÕAD£¨
°ý°œAQD£Ω90°„£¨
°ý°œDOQ+°œAOQ£Ω90°„£¨°œAOQ+°œOAQ£Ω90°„£¨
°ý°œDOQ£Ω°œOAQ£¨
°ýtam°œOAD£Ωtan°œDOC£Ω![]() £¨
£¨
°ý![]() £Ω
£Ω![]() £¨
£¨
°ý![]() £Ω
£Ω![]() £¨
£¨
°ým£Ω![]() £Æ
£Æ
◊€…œÀ˘ ˆ£¨¬˙◊„Ãıº˛µƒmµƒ÷µŒ™![]() ªÚ
ªÚ![]() £Æ
£Æ
¢⁄»ÁÕº4÷–£¨◊˜BG°ÕBCΩªOCµƒ—”≥§œþ”⁄G£¨¡¨Ω”DF£¨AF£¨◊˜BH°ÕOG”⁄H£¨◊˜FP°ÕOA”⁄P£Æ
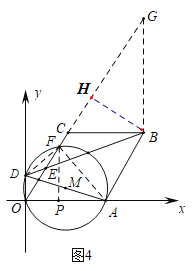
°þBC//OA£¨
°ýtan°œGCB£Ωtan°œCOA£Ω![]() £Ω
£Ω![]() £¨
£¨
°ýBG£Ω![]() £¨
£¨
°þOD//BG£¨
°ý°œG£Ω°œDOE£¨
°þDO£ΩED£¨
°ý°œDOE£Ω°œDEO£Ω°œBEG£¨
°ý°œG£Ω°œBEG£¨
°ýBE£ΩBG£Ω![]() £¨
£¨
°þDE+BE£ΩBD£¨
°ý(m+![]() )2£Ω82+(4©Åm)2£¨
)2£Ω82+(4©Åm)2£¨
Ω‚µ√m£Ω![]() £¨
£¨
…ËOF£Ω5k£¨‘ÚFP£Ω4k£¨OP£Ω3k£¨
°þ°œODF£Ω°œDAF£¨
°ýtan°œDAF£Ω![]() £Ω
£Ω![]() £¨
£¨
°ýsin°œDAF£Ω![]() £¨
£¨
°þAD£Ω![]() £Ω
£Ω![]() £¨
£¨
°ýAF£Ω![]()
![]() £¨
£¨
‘⁄Rt°˜APF÷–£¨°þAF2£ΩPF2+PA2£¨
°ý![]() °¡(m2+25)£Ω(4k)2+(5©Å3k)2£¨
°¡(m2+25)£Ω(4k)2+(5©Å3k)2£¨
∞—m£Ω![]() ¥˙»Î£¨’˚¿Ìµ√£∫45k2©Å54k+13£Ω0£¨
¥˙»Î£¨’˚¿Ìµ√£∫45k2©Å54k+13£Ω0£¨
Ω‚µ√k£Ω![]() £®…·»•£©ªÚ
£®…·»•£©ªÚ![]() £¨
£¨
°ýOF£Ω![]() £Æ
£Æ
°þsin°œG£Ωsin°œDAF£Ω![]() £¨
£¨
°ýGH=![]() £¨
£¨
°ýEG=2GH=![]() £¨
£¨
°þBG//OD£¨
°ý°˜ODE°◊°˜GBE£¨
°ý![]() £¨
£¨
°þOE£Ω![]() £¨
£¨
°ýEF£ΩOF©ÅOE£Ω![]() £¨
£¨
°ý![]() £Ω
£Ω![]() £Ω
£Ω![]() £Æ
£Æ


 ÃÏÃϜڅœ“ª±æ∫√æÌœµ¡–¥∞∏
ÃÏÃϜڅœ“ª±æ∫√æÌœµ¡–¥∞∏ –°—ß…˙10∑÷÷””¶”√Âœµ¡–¥∞∏
–°—ß…˙10∑÷÷””¶”√Âœµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨’˝¡˘±þ–Œ ABCDEFµƒ÷––ƒ”Î◊¯±Í‘≠µ„O÷ÿ∫œ£¨∆‰÷–A(-2£¨0)£ÆΩ´¡˘±þ–Œ ABCDEF»∆‘≠µ„O∞¥À≥ ±’Î∑ΩœÚ–˝◊™2018¥Œ£¨√ø¥Œ–˝◊™60°„£¨‘Ú–˝◊™∫Ûµ„Aµƒ∂‘”¶µ„A'µƒ◊¯±Í «£® £©£Æ
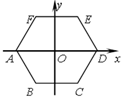
A. (1£¨![]() ) B. (
) B. (![]() £¨1) C. (1£¨
£¨1) C. (1£¨![]() ) D. (-1£¨
) D. (-1£¨![]() )
)
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“ªµ¿◊˜ÕºÃ‚»Áœ¬£∫
“—÷™£∫»ÁÕº1£¨°œABCº∞BC±þ…œ“ªµ„D£Æ
«Û◊˜£∫“ªµ„P£¨ πµ„PµΩ°œABC¡Ω±þµƒæý¿Îœýµ»£¨«“µΩB£¨D¡Ωµ„µƒæý¿Îœýµ»£Æœ¬√Ê «“ªŒªÕ¨—ßµƒ◊˜Õºπ˝≥ã®Õº2£©£∫
£®1£©◊˜°œABCµƒ∆Ω∑÷œþBE£ª
£®2£©◊˜œþ∂ŒBDµƒ¥π÷±∆Ω∑÷œþl£¨”ÎBEΩª”⁄µ„P£Æ
À˘“‘µ„PæÕ «À˘«Û◊˜µƒµ„£Æ‘Ú∏√◊˜Õºµƒ“¿æð «___________________________________£Æ
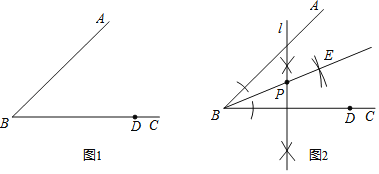
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
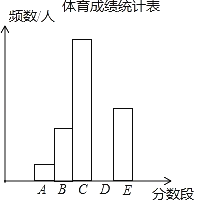
°æƒø°øŒ™¡À¡ÀΩ‚ƒ≥ –æ≈ƒÍº∂—ß…˙µƒÃ”˝≥…º®£®≥…º®æ˘Œ™’˚ ˝£©£¨Àʪ˙≥È»°¡À≤ø∑÷—ß…˙µƒÃ”˝≥…º®≤¢∑÷∂Œ£®A£∫20.5°´22.5£ªB£∫22.5°´24.5£ªC£∫24.5°´26.5£ªD£∫26.5°´28.5£ªE£∫28.5°´30.5£©Õ≥º∆£¨µ√µΩÕ≥º∆Õº°¢±Ì»ÁÕº£Æ
∑÷ ˝∂Œ | A | B | C | D | E | ∫œº∆ |
∆µ ˝/»À | 12 | 36 | 84 | b | 48 | c |
Ƶ | 0.05 | a | 0.35 | 0.25 | 0.20 | 1 |
∏˘æð…œ√ʵƒ–≈œ¢£¨ªÿ¥œ¬¡–Œ £∫
£®1£©Õ≥º∆±Ì÷–£¨a£Ω°° °°£¨b£Ω°° °°£¨c£Ω°° °°£ªΩ´∆µ ˝∑÷≤º÷±∑ΩÕº≤π≥‰ÕÍ’˚£Æ
£®2£©–°√˜Àµ£∫°∞’‚◊È ˝æðµƒ÷⁄ ˝“ª∂®‘⁄C÷–£Æ°±ƒ„»œŒ™–°√˜µƒÀµ∑®’˝»∑¬£ø°° °°£®—°ÃÓ°∞’˝»∑°±ªÚ°∞¥ÌŒÛ°±£©£Æ
£®3£©»Ù≥…º®‘⁄27∑÷º∞“‘…œ∂®Œ™”≈–„£¨‘Ú∏√ –30000√˚æ≈ƒÍº∂—ß…˙÷–Ô˝≥…º®Œ™”≈–„µƒ—ß…˙»À ˝‘º”–∂ý…Ÿ£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
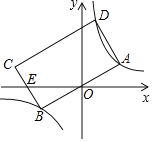
°æƒø°ø»ÁÕº£¨æÿ–ŒABCDµƒ∂•µ„A£¨B£¨D∑÷±¬‰‘⁄À´«˙œþy£Ω![]() £®k£æ0£©µƒ¡Ω∏ˆ∑÷÷ß…œ£¨AB±þæ≠π˝‘≠µ„O£¨CB±þ”Îx÷·Ωª”⁄µ„E£¨«“EC£ΩEB£¨»Ùµ„Aµƒ∫·◊¯±ÍŒ™1£¨‘Úæÿ–ŒABCDµƒ√ʪ˝_____£Æ
£®k£æ0£©µƒ¡Ω∏ˆ∑÷÷ß…œ£¨AB±þæ≠π˝‘≠µ„O£¨CB±þ”Îx÷·Ωª”⁄µ„E£¨«“EC£ΩEB£¨»Ùµ„Aµƒ∫·◊¯±ÍŒ™1£¨‘Úæÿ–ŒABCDµƒ√ʪ˝_____£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨≈◊ŒÔœþ ![]() ”Î
”Î ![]() ÷·Ωª”⁄
÷·Ωª”⁄![]() ∫Õ
∫Õ![]() £¨”Î
£¨”Î ![]() ÷·Ωª”⁄
÷·Ωª”⁄ ![]() µ„£¨µ„
µ„£¨µ„![]() πÿ”⁄≈◊ŒÔœþµƒ∂‘≥∆÷·µƒ∂‘≥∆µ„Œ™µ„
πÿ”⁄≈◊ŒÔœþµƒ∂‘≥∆÷·µƒ∂‘≥∆µ„Œ™µ„![]() £Æ
£Æ
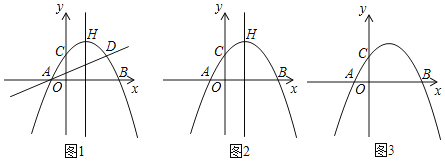
£®1£©«Û¥À≈◊ŒÔœþµƒΩ‚Œˆ Ω∫Õ∂‘≥∆÷·£Æ
£®2£©»ÁÕº 2£¨µ±µ„![]() ‘⁄≈◊ŒÔœþµƒ∂‘≥∆÷·…œ‘À∂Ø ±£¨‘⁄÷±œþ
‘⁄≈◊ŒÔœþµƒ∂‘≥∆÷·…œ‘À∂Ø ±£¨‘⁄÷±œþ![]() …œ «∑ҥʑ⁄µ„
…œ «∑ҥʑ⁄µ„![]() £¨ πµ√“‘µ„
£¨ πµ√“‘µ„![]() °¢
°¢![]() °¢
°¢![]() °¢
°¢![]() Œ™∂•µ„µƒÀƒ±þ–ŒŒ™∆Ω––Àƒ±þ–Œ£ø»Ù¥Ê‘⁄£¨«Î«Û≥ˆµ„
Œ™∂•µ„µƒÀƒ±þ–ŒŒ™∆Ω––Àƒ±þ–Œ£ø»Ù¥Ê‘⁄£¨«Î«Û≥ˆµ„ ![]() µƒ◊¯±Í£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
µƒ◊¯±Í£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
£®3£©»ÁÕº 3£¨µ±µ„![]() °¢
°¢![]() °¢
°¢![]() »˝µ„π≤‘≤ ±£¨«Î«Û≥ˆ∏√‘≤‘≤–ƒµƒ◊¯±Í£Æ
»˝µ„π≤‘≤ ±£¨«Î«Û≥ˆ∏√‘≤‘≤–ƒµƒ◊¯±Í£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øÀ≥¥Œ¡¨Ω”∂‘Ω«œþœýµ»µƒÀƒ±þ–Œ∏˜±þ÷–µ„£¨À˘µ√Àƒ±þ–Œ «( )
A. æÿ–Œ B. ∆Ω––Àƒ±þ–Œ C. ¡‚–Œ D. »Œ“‚Àƒ±þ–Œ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥…õ͜˙ €10îA–Õ∫Õ20îB–ÕµÁƒ‘µƒ¿˚»ÛŒ™4000‘™£¨œ˙ €20îA–Õ∫Õ10îB–ÕµÁƒ‘µƒ¿˚»ÛŒ™3500‘™£Æ
£®1£©«Û√øîA–ÕµÁƒ‘∫ÕB–ÕµÁƒ‘µƒœ˙ €¿˚»Û£ª
£®2£©∏√…õͺ∆ªÆ“ª¥Œπ∫Ω¯¡Ω÷÷–Õ∫≈µƒµÁƒ‘π≤100∆‰÷–B–ÕµÁƒ‘µƒΩ¯ªı¡ø≤ª≥¨π˝A–ÕµÁƒ‘µƒ2±∂£¨…Ëπ∫Ω¯A–ÕµÁƒ‘x’‚100îµÁƒ‘µƒœ˙ €◊п˚»ÛŒ™y‘™£Æ
¢Ÿ«Ûyπÿ”⁄xµƒ∫Ø ˝πÿœµ Ω£ª
¢⁄∏√…õÍπ∫Ω¯A–Õ°¢B–ÕµÁƒ‘∏˜∂ý…ŸÃ®£¨≤≈ƒÐ πœ˙ €◊п˚»Û◊Ó¥Û£ø
£®3£© µº Ω¯ªı ±£¨≥ߺ“∂‘A–ÕµÁƒ‘≥ˆ≥ߺ€œ¬µ˜m£®0£ºm£º100£©‘™£¨«“œÞ∂®…õÍ◊Ó∂ýπ∫Ω¯A–ÕµÁƒ‘70»Ù…õͱ£≥÷Õ¨÷÷µÁƒ‘µƒ €º€≤ª±‰£¨«Îƒ„∏˘æð“‘…œ–≈œ¢º∞£®2£©÷–Ãıº˛£¨…˺∆≥ˆ π’‚100îµÁƒ‘œ˙ €◊п˚»Û◊Ó¥ÛµƒΩ¯ªı∑Ω∞∏£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
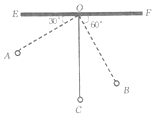
°æƒø°ø»ÁÕº£¨ŒÔ¿ÌΩà ¶Œ™Õ¨—ß√«—ð 浕∞⁄‘À∂Ø£¨µ•∞⁄◊Û”“∞⁄∂Ø÷–£¨‘⁄![]() µƒŒª÷√ ±∏©Ω«
µƒŒª÷√ ±∏©Ω«![]() £¨‘⁄
£¨‘⁄![]() µƒŒª÷√ ±∏©Ω«
µƒŒª÷√ ±∏©Ω«![]() £¨»Ù
£¨»Ù![]() £¨µ„
£¨µ„![]() ±»µ„
±»µ„![]() ∏þ7
∏þ7![]() £Æ
£Æ
«Û£∫£®1£©µ•∞⁄µƒ≥§∂»£ª
£®2£©¥”µ„![]() ∞⁄∂ØµΩµ„
∞⁄∂ØµΩµ„![]() æ≠π˝µƒ¬∑æ∂≥§£Æ£®“™«Û£∫±æÂ÷–µƒº∆À„Ω·π˚æ˘±£¡Ù’˚ ˝£Æ≤Œøº÷µ£∫
æ≠π˝µƒ¬∑æ∂≥§£Æ£®“™«Û£∫±æÂ÷–µƒº∆À„Ω·π˚æ˘±£¡Ù’˚ ˝£Æ≤Œøº÷µ£∫![]() £ª
£ª![]() £©
£©
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com