
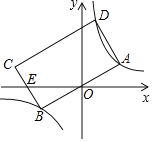
【题目】如图,矩形ABCD的顶点A,B,D分别落在双曲线y=![]() (k>0)的两个分支上,AB边经过原点O,CB边与x轴交于点E,且EC=EB,若点A的横坐标为1,则矩形ABCD的面积_____.
(k>0)的两个分支上,AB边经过原点O,CB边与x轴交于点E,且EC=EB,若点A的横坐标为1,则矩形ABCD的面积_____.
【答案】![]() .
.
【解析】
过点B作BM⊥x轴于点M,过点C作CN⊥x轴于点N,过点A作AF⊥x轴于点F,设A点坐标为(1,a),则OB、BE、EM均可用a表示,易知△CNE≌△BME,通过线段等量关系可求用a表示的C点坐标,继而求得D点坐标,根据A、D都在反比例函数图象上,得到关于a的方程,求解a值,再求出AB和BC值,则矩形面积可求.
设A点坐标为(1,a),过点B作BM⊥x轴于点M,过点C作CN⊥x轴于点N,过点A作AF⊥x轴于点F,如下图所示,
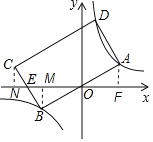
由A(1,a),
由对称性质有B(﹣1,﹣a),BM=AF=a,OM=OF=1,
∴OB=OA=![]() ,
,
∵tan∠BOE=tan∠AOF,
∴![]() ,即
,即![]() ,
,
∴BE=![]() ,
,
∴![]() ,
,
∵BE=CE,∠CEN=∠BEM,∠CNE=∠BME,
∴△CNE≌△BME,
∴CN=BM=a,NE=EM=a2,CE=BE=![]() ,
,
∴ON=2a2+1,
∴C(﹣2a2﹣1,a),
∵A(1,a),B(﹣1,﹣a),BC//AD,AD=BC,
∴D(1﹣2a2,3a),
∵A、D都在反比例函数图象上,
∴3a(1﹣2a2)=a1,
解得a=![]() ,
,
∴AB=2OA=2![]() =
=![]() ,BC=2BE=2a
,BC=2BE=2a![]() =
=![]() ,
,
∴矩形ABCD的面积 ![]() .
.
故答案为:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与 x 轴交于点 A、B,与 y 轴交于点 C,且 OC=2OB, 点 D 为线段 OB 上一动点(不与点 B 重合),过点 D 作矩形 DEFH,点 H、F 在抛物线上,点 E 在 x 轴 上.
与 x 轴交于点 A、B,与 y 轴交于点 C,且 OC=2OB, 点 D 为线段 OB 上一动点(不与点 B 重合),过点 D 作矩形 DEFH,点 H、F 在抛物线上,点 E 在 x 轴 上.
(1)求抛物线的解析式;
(2)当矩形 DEFH 的周长最大时,求矩形 DEFH 的面积;
(3)在(2)的条件下,矩形 DEFH 不动,将抛物线沿着 x 轴向左平移 m 个单位,抛物线与矩形 DEFH的边交于点 M、N,连接 M、N.若 MN 恰好平分矩形 DEFH 的面积,求 m 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】题目:为了美化环境,某地政府计划对辖区内![]() 的土地进行绿化.为了尽快完成任务,实际平均每月的绿化面积是原计划的1.5倍,结果提前2个月完成任务.求原计划平均每月的绿化面积.
的土地进行绿化.为了尽快完成任务,实际平均每月的绿化面积是原计划的1.5倍,结果提前2个月完成任务.求原计划平均每月的绿化面积.
甲同学所列的方程为![]()
乙同学所列的方程为![]()
(1)甲同学所列的方程中![]() 表示 .乙同学所列的方程中
表示 .乙同学所列的方程中![]() 表示 .
表示 .
(2)任选甲、乙两同学的其中一个方法解答这个题目.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与直线
两点,与直线![]() 交于
交于![]() 、
、![]() 两点,直线
两点,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(1)求直线![]() 的解析式:
的解析式:
(2)若点![]() 在线段
在线段![]() 上以每秒1个单位长度的速度从点
上以每秒1个单位长度的速度从点![]() 向点
向点![]() 运动(不与点
运动(不与点![]() 、
、![]() 重合),同时,点
重合),同时,点![]() 在射线
在射线![]() 上以每秒2个单位长度的速度从点
上以每秒2个单位长度的速度从点![]() 向点
向点![]() 方向运动,设运动的时间为
方向运动,设运动的时间为![]() 秒,
秒,![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的函数关系式,并求
的函数关系式,并求![]() 取何值时,
取何值时,![]() 最大?最大值是多少?
最大?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现:如图1,在![]() 和
和![]() 中,
中,![]() ,连接
,连接![]() 交于点
交于点![]() .求证:
.求证:![]() ;并直接写出
;并直接写出![]() ______.
______.
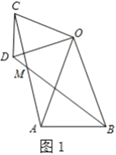
(2)类比探究:如图2,在![]() 和
和![]() 中,
中,![]() ,连接
,连接![]() 交
交![]() 的延长线于点
的延长线于点![]() .请判断
.请判断![]() 的值及
的值及![]() 的度数.
的度数.
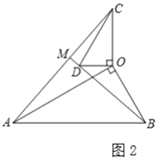
(3)拓展延伸:在(2)的条件下,将![]() 绕点
绕点![]() 在平面内旋转,
在平面内旋转,![]() 所在直线
所在直线![]() 交于点.若
交于点.若![]() ,请直接写出当点
,请直接写出当点![]() 与点
与点![]() 重合时
重合时![]() 的长.
的长.
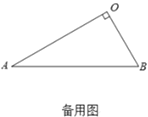
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图点A,E,F,C在同一直线上,AE=EF=FC,过E,F分别作DE⊥AC,BF⊥AC,连结AB,CD,BD,BD交AC于点G,若AB=CD.
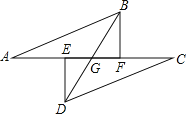
(1)求证:△ABF≌△CDE.
(2)若AE=ED=2,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为防控“新型冠状病毒”,某超市分别用1600元、6000元购进两批防护口罩,第二批防护口罩的数量是第一批的3倍,但单价比第一批贵2元.
(1)第一批口罩进货单价多少元?
(2)若这两次购买防护口罩过程中所产生其他费用不少于600元,那么该超市购买这两批防护口罩的平均单价至少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司推出一款产品,经市场调查发现,该产品的日销售量y(个)与销售单价x(元)之间满足一次函数关系,关于销售单价,日销售量,日销售利润的几组对应值如表:
销售单价x(元) | 85 | 95 | 105 | 115 |
日销售量y(个) | 175 | 125 | 75 | 25 |
日销售利润w(元) | 875 | 1875 | 1875 | 875 |
(注:日销售利润=日销售量×(销售单价﹣成本单价))
(1)求y与x的函数关系式;
(2)当销售单价x为多少元时,日销售利润w最大?最大利润是多少元?
(3)当销售单价x为多少元时,日销售利润w在1500元以上?(请直接写出x的范围)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高学生的阅读能力,我市某校开展了“读好书,助成长”的活动,并计划购置一批图书,购书前,对学生喜欢阅读的图书类型进行了抽样调查,并将调查数据绘制成两幅不完整的统计图,如图所示,请根据统计图回答下列问题:
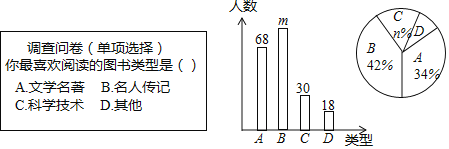
(1)本次调查共抽取了 名学生,两幅统计图中的m= ,n= .
(2)已知该校共有3600名学生,请你估计该校喜欢阅读“A”类图书的学生约有多少人?
(3)学校将举办读书知识竞赛,九年级1班要在本班3名优胜者(2男1女)中随机选送2人参赛,请用列表或画树状图的方法求被选送的两名参赛者为一男一女的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com