
【题目】已知:如图点A,E,F,C在同一直线上,AE=EF=FC,过E,F分别作DE⊥AC,BF⊥AC,连结AB,CD,BD,BD交AC于点G,若AB=CD.
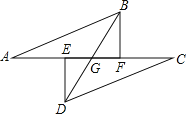
(1)求证:△ABF≌△CDE.
(2)若AE=ED=2,求BD的长.
科目:初中数学 来源: 题型:
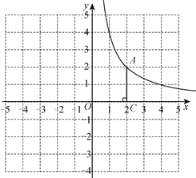
【题目】如图,在平面直角坐标系xOy中,函数![]() 的图象经过点
的图象经过点![]() ,作AC⊥x轴于点C.
,作AC⊥x轴于点C.
(1)求k的值;
(2)直线AB:![]() 图象经过点
图象经过点![]() 交x轴于点
交x轴于点![]() .横、纵坐标都是整数的点叫做整点.线段AB,AC,BC围成的区域(不含边界)为W.
.横、纵坐标都是整数的点叫做整点.线段AB,AC,BC围成的区域(不含边界)为W.
①直线AB经过![]() 时,直接写出区域W内的整点个数;
时,直接写出区域W内的整点个数;
②若区域W内恰有1个整点,结合函数图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在平面直角坐标系中,![]() 为坐标原点,
为坐标原点,![]() 的边
的边![]() 平行于
平行于![]() 轴.若
轴.若![]() 的三个顶点都在二次函数
的三个顶点都在二次函数![]() 的图像上,则称
的图像上,则称![]() 为该二次函数图像的“伴随三角形”.
为该二次函数图像的“伴随三角形”.![]() 为抛物
为抛物![]() 的“伴随三角形”.
的“伴随三角形”.
(1)若点![]() 是抛物线与
是抛物线与![]() 轴的交点,求点
轴的交点,求点![]() 的坐标.
的坐标.
(2)若点![]() 在该抛物线的对称轴上,且到边
在该抛物线的对称轴上,且到边![]() 的距离为2,求
的距离为2,求![]() 的面积.
的面积.
(3)设![]() 两点的坐标分别为
两点的坐标分别为![]() ,比较
,比较![]() 与
与![]() 的大小,并求
的大小,并求![]() 的取值范围.
的取值范围.
(4)![]() 是抛物线
是抛物线![]() 的“伴随三角形”,点
的“伴随三角形”,点![]() 在点
在点![]() 的左侧,且
的左侧,且![]() ,点
,点![]() 的横坐标是点
的横坐标是点![]() 的横坐标的2倍,设该抛物线在
的横坐标的2倍,设该抛物线在![]() 上最高点的纵坐标为
上最高点的纵坐标为![]() ,当
,当![]() 时,直接写出
时,直接写出![]() 的取值范围和
的取值范围和![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学老师为了了解学生在数学学习中常见错误的纠正情况,收集整理了学生在作业和考试中的常见错误,编制了10道选择题,每题3分,对他所教的初三(1)班、(2)班进行了检测,如图表示从两班各随机抽取的10名学生的得分情况.
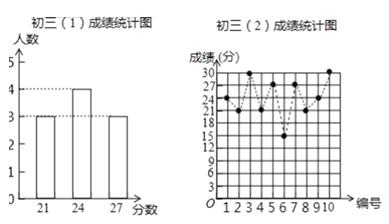
(1)利用图中提供的信息,补全下表:
班级 | 平均数/分 | 中位数/分 | 众数/分 | 方差/分 |
初三(1)班 | 24 | 24 | ________ | 5.4 |
初三(2)班 | 24 | _________ | 21 | ________ |
(2)哪个班的学生纠错的得分更稳定?若把24分以上(含24分)记为“优秀”,两班各40名学生,请估计两班各有多少名学生成绩优秀;
(3)现从两个班抽取了数学成绩最好的甲、乙、丙、丁四位同学,并随机分成两组进行数学竞赛,求恰好选中甲、乙一组的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的顶点A,B,D分别落在双曲线y=![]() (k>0)的两个分支上,AB边经过原点O,CB边与x轴交于点E,且EC=EB,若点A的横坐标为1,则矩形ABCD的面积_____.
(k>0)的两个分支上,AB边经过原点O,CB边与x轴交于点E,且EC=EB,若点A的横坐标为1,则矩形ABCD的面积_____.
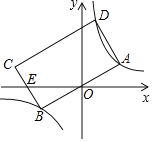
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校团委举办了一次“中国梦,我的梦”演讲比赛,满分10分,学生得分均为整数,成绩达6分以上(含6分)为合格,达9分以上(含9分)为优秀.这次竞赛中甲,乙两组学生成绩分布的条形统计图如下:
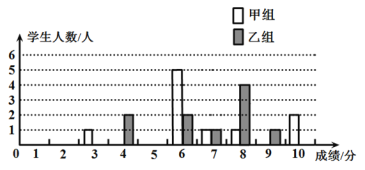
(1)将下表补充完整:
组别 | 平均分 | 中位数 | 众数 | 方差 | 合格率 | 优秀率 |
甲 | 6.8 |
| 6 | 3.96 | 90% | 20% |
乙 |
| 7.5 |
| 2.76 | 80% | 10% |
(2)小明同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上表可知,小明是 组学生(填“甲””或“乙”);
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你给出两条支持乙组同学观点的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
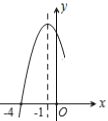
【题目】二次函数![]() 的部分图象如图所示,图象过点
的部分图象如图所示,图象过点![]() ,对称轴为直线
,对称轴为直线![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③一元二次方程
;③一元二次方程![]() 的解是
的解是![]() ,
,![]() ;④当
;④当![]() 时,
时,![]() ,其中正确的结论有__________.
,其中正确的结论有__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com