
【题目】如图,在平面直角坐标系中,直线![]() 交坐标轴于
交坐标轴于![]() 、
、![]() 点,点
点,点![]() 在线段
在线段![]() 上,以
上,以![]() 为一边在第一象限作正方形
为一边在第一象限作正方形![]() .若双曲线
.若双曲线![]() 经过点
经过点![]() ,
,![]() .则
.则![]() 的值为__________.
的值为__________.

【答案】8
【解析】
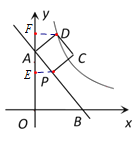
作PE⊥OA于E,作DF⊥OA于F.通过证明△EAP≌△FDA,可得DF=AE,AF=PE.根据勾股定理求出AE的长,进而求出点D的坐标,即可求出k的值.
作PE⊥OA于E,作DF⊥OA于F.
∵四边形APCD是正方形,
∴AP=AD=CD=2, ∠PAD=90°.
∵∠EAP+∠DAF=90°, ∠ADF+∠DAF=90°,
∴∠EAP=∠ADF.
在△EAP和△FDA中,
∵∠EAP=∠ADF,
∠AEP=∠AFD=90°,
AP=AD,
∴△EAP≌△FDA,
∴DF=AE,AF=PE.
∵![]() ,
,
∴AF=PE=![]() ,
,
∴AE=![]() =
=![]() ,
,
∴OF=![]() +
+![]() +
+![]() =5,
=5,
∴DF=![]() ,
,
∴D(![]() ,5),
,5),
∴k=![]() ×5=8.
×5=8.
故答案为:8.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() 为射线
为射线![]() 上一定点,点
上一定点,点![]() 关于射线
关于射线![]() 的对称点为点
的对称点为点![]() 为射线
为射线![]() 上一动点,连接
上一动点,连接![]() ,满足
,满足![]() 为钝角,以点
为钝角,以点![]() 为中心,将线段
为中心,将线段![]() 逆时针旋转
逆时针旋转![]() 至线段
至线段![]() ,满足点
,满足点![]() 在射线
在射线![]() 的反向延长线上.
的反向延长线上.
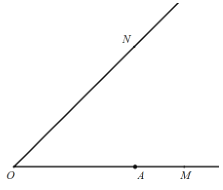
(1)依题意补全图形;
(2)当点![]() 在运动过程中,旋转角
在运动过程中,旋转角![]() 是否发生变化?若不变化,请求出
是否发生变化?若不变化,请求出![]() 的值,若变化,请说明理由;
的值,若变化,请说明理由;
(3)从点![]() 向射线
向射线![]() 作垂线,与射线
作垂线,与射线![]() 的反向延长线交于点
的反向延长线交于点![]() ,探究线段
,探究线段![]() 和
和![]() 的数量关系并证明.
的数量关系并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两个工厂同时加工一批机器零件.甲工厂先加工了两天后停止加工,维修设备,当维修完设备时,甲乙两厂加工的零件数相等,甲工厂再以原来的工作效率继续加工这批零件.甲乙两厂加工零件的数量![]() (件),
(件),![]() (件)与加工件的时间
(件)与加工件的时间![]() (天)的函数图象如图所示,
(天)的函数图象如图所示,

(1)乙工厂每天加工零件的数为_____件;
(2)甲工厂维修设备的时间是多少天?
(3)求甲维修设备后加工零件的数量![]() (件)与加工零件的时间
(件)与加工零件的时间![]() (天)的函数关系式,并写出自变量
(天)的函数关系式,并写出自变量![]() 的取值范围
的取值范围
查看答案和解析>>
科目:初中数学 来源: 题型:
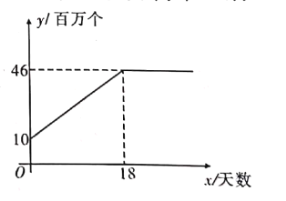
【题目】随着新冠肺炎的爆发,市场对口罩的需求量急剧增大.某口罩生产商自二月份以来,--直积极恢复产能,每日口罩生产量![]() (百万个)与天数
(百万个)与天数![]() 且
且![]() 为整数)的函数关系图象如图所示,而该生产商对口供应市场对口罩的需求量<(百万个)与天数
为整数)的函数关系图象如图所示,而该生产商对口供应市场对口罩的需求量<(百万个)与天数![]() 呈抛物线型,第
呈抛物线型,第![]() 天市场口罩缺口(需求量与供应量差)就达到
天市场口罩缺口(需求量与供应量差)就达到![]() (百万个),之后若干天,市场口罩需求量不断上升,在第
(百万个),之后若干天,市场口罩需求量不断上升,在第![]() 天需求量达到最高峰
天需求量达到最高峰![]() (百万个).
(百万个).
![]() 求出
求出![]() 与
与![]() 的函数解析式;
的函数解析式;
![]() 当市场供应量不小于需求量时,市民买口罩才无需提前预约,那么在整个二月份,市民无需预约即可购买口罩的天数共有多少天?
当市场供应量不小于需求量时,市民买口罩才无需提前预约,那么在整个二月份,市民无需预约即可购买口罩的天数共有多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
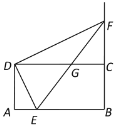
【题目】已知:如图点A,E,F,C在同一直线上,AE=EF=FC,过E,F分别作DE⊥AC,BF⊥AC,连结AB,CD,BD,BD交AC于点G,若AB=CD.
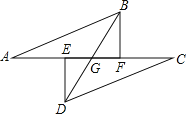
(1)求证:△ABF≌△CDE.
(2)若AE=ED=2,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在
在![]() 边上,与点
边上,与点![]() 、
、![]() 不重合,过点
不重合,过点![]() 作
作![]() 的垂线与
的垂线与![]() 的延长线相交于点
的延长线相交于点![]() ,连结
,连结![]() ,交
,交![]() 于点
于点![]() .
.
(1)当![]() 为
为![]() 的中点时,求
的中点时,求![]() 的长;
的长;
(2)当![]() 是以
是以![]() 为腰的等腰三角形时,求
为腰的等腰三角形时,求![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形纸片ABCD中,已知AD=8,AB=6,E是边BC上的点,以AE为折痕折叠纸片,使点B落在点F处,连接FC,当△EFC为直角三角形时,BE的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
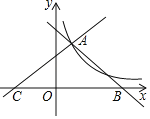
【题目】如图直线y1=﹣x+4,y2=![]() x+b都与双曲线y=
x+b都与双曲线y=![]() 交于点A(1,3),这两条直线分别与x轴交于B,C两点.
交于点A(1,3),这两条直线分别与x轴交于B,C两点.
(1)求k的值;
(2)直接写出当x>0时,不等式![]() x+b>
x+b>![]() 的解集;
的解集;
(3)若点P在x轴上,连接AP,且AP把△ABC的面积分成1:2两部分,则此时点P的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】富贵竹茎叶肥厚,观赏价值高,又有“花开富贵,竹报平安,大吉大利”之意,深受广大花友的喜爱.某花店抓住这个商机,第一次购进![]() 、
、![]() 两种造型的富贵竹共300株.
两种造型的富贵竹共300株.![]() 型富贵竹每盆成本4元,售价8元;
型富贵竹每盆成本4元,售价8元;![]() 型富贵竹每盆成本7元,售价10元.
型富贵竹每盆成本7元,售价10元.
(1)如果第一次购进富贵竹的金额为1500元,那么![]() 型富贵竹购进了多少盆?
型富贵竹购进了多少盆?
(2)富贵竹开始售卖后,十分抢手,花店决定第二次购进这两种造型的富贵竹,它们的进价不变.![]() 型富贵竹的进货量在第一次进货量的基础上增加了
型富贵竹的进货量在第一次进货量的基础上增加了![]() ,售价提高了
,售价提高了![]() ;
;![]() 型富贵竹的售价和进货量不变.结果第二次共获利2100元.求
型富贵竹的售价和进货量不变.结果第二次共获利2100元.求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com