
【题目】如图,在平面直角坐标系xOy中,函数![]() 的图象经过点
的图象经过点![]() ,作AC⊥x轴于点C.
,作AC⊥x轴于点C.
(1)求k的值;
(2)直线AB:![]() 图象经过点
图象经过点![]() 交x轴于点
交x轴于点![]() .横、纵坐标都是整数的点叫做整点.线段AB,AC,BC围成的区域(不含边界)为W.
.横、纵坐标都是整数的点叫做整点.线段AB,AC,BC围成的区域(不含边界)为W.
①直线AB经过![]() 时,直接写出区域W内的整点个数;
时,直接写出区域W内的整点个数;
②若区域W内恰有1个整点,结合函数图象,求a的取值范围.
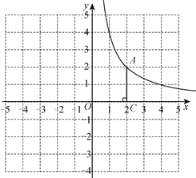
【答案】(1)k=4; (2)①1个; ②当![]() 时区域W内恰有1个整点.
时区域W内恰有1个整点.
【解析】
(1)把A(2,2)代入y=![]() 中便可求得k;
中便可求得k;
(2)①根据图象直接写出答案便可;
②用待定系数法求出直线AB分别过点(0,1),(1,0),(3,1),(4,1)四点时的a值便可.
解:(1)把A(2,2)代入y=![]() 中,得k=2×2=4;
中,得k=2×2=4;
(2)①∵直线AB经过(0,1),设直线AB的解析式为:y=ax+b(a≠0),则
![]() ,
,
解得![]() ,
,
∴直线AB的解析式为:y=![]() x+1,
x+1,
∴B(-2,0),
图象如下:
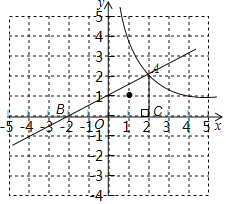
由图象可知,直线AB经过(0,1)时,区域W内的整点只有1个;
②当直线AB经过点A(2,2),(0,1)时区域W内恰有1个整点,则
![]() ,
,
∴a=![]() ,
,
当直线AB经过点A(2,2),(1,1)时区域W内没有整点,则
![]() ,
,
∴a=1,
∴当![]() ≤a<1时区域W内恰有1个整点;
≤a<1时区域W内恰有1个整点;
综上,当![]() ≤a<1时区W内恰有1个整点.
≤a<1时区W内恰有1个整点.


科目:初中数学 来源: 题型:
【题目】如图(1),二次函数![]() 的图象与
的图象与![]() 轴、直线
轴、直线![]() 的交点分别为点
的交点分别为点![]() 、
、![]() .
.

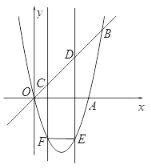

图(1) 图(2) (备用图)
(1)![]()
![]() _________,
_________,![]()
![]() _________,
_________,![]() =_________
=_________![]() ;
;
(2)连接AB,点![]() 是抛物线上一点(异于点A),且
是抛物线上一点(异于点A),且![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)如图(2),点![]() 、
、![]() 是线段
是线段![]() 上的动点,且
上的动点,且![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() .
.
①过点![]() 、
、![]() 分别作
分别作![]() 轴的垂线,与抛物线相交于点
轴的垂线,与抛物线相交于点![]() 、
、![]() ,连接
,连接![]() .当
.当![]() 取得最大值时,求
取得最大值时,求![]() 的值并判断四边形
的值并判断四边形![]() 的形状;
的形状;
②连接![]() 、
、![]() ,求
,求![]() 为何值时,
为何值时,![]() 取得最小值,并求出这个最小值.
取得最小值,并求出这个最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
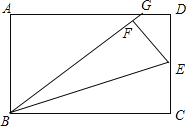
【题目】如图,在矩形ABCD中,点E是CD的中点,将△BCE沿BE折叠后得到△BEF、且点F在矩形ABCD的内部,将BF延长交AD于点G.若![]() ,则
,则![]() =__.
=__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=![]() x2+mx+n与x轴相交于点A、B两点,过点B的直线y=x+b交抛物线于另一点C(-5,6),点D是线段BC上的一个动点(点D与点B、C不重合),作DE∥AC,交该抛物线于点E,
x2+mx+n与x轴相交于点A、B两点,过点B的直线y=x+b交抛物线于另一点C(-5,6),点D是线段BC上的一个动点(点D与点B、C不重合),作DE∥AC,交该抛物线于点E,
(1)求m,n,b的值;
(2)求tan∠ACB;
(3)探究在点D运动过程中,是否存在∠DEA=45°,若存在,则求此时线段AE的长;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,对于两个点
中,对于两个点![]() ,
,![]() 和图形
和图形![]() ,如果在图形
,如果在图形![]() 上存在点
上存在点![]() ,
,![]() (
(![]() ,
,![]() 可以重合)使得
可以重合)使得![]() ,那么称点
,那么称点![]() 与点
与点![]() 是图形
是图形![]() 的一对平衡点.
的一对平衡点.
(1)如图1,已知点![]() ,
,![]() ;
;
①设点![]() 与线段
与线段![]() 上一点的距离为
上一点的距离为![]() ,则
,则![]() 的最小值是 ,最大值是 ;
的最小值是 ,最大值是 ;
②在![]() ,
,![]() ,
,![]() 这三个点中,与点
这三个点中,与点![]() 是线段
是线段![]() 的一对平衡点的是 ;
的一对平衡点的是 ;
(2)如图2,已知![]() 的半径为1,点
的半径为1,点![]() 的坐标为
的坐标为![]() 在第一象限,且点
在第一象限,且点![]() 与点
与点![]() 是
是![]() 的一对平衡点,求
的一对平衡点,求![]() 的取值范围;
的取值范围;
(3)如图3,已知点![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 长为半径画弧交
长为半径画弧交![]() 的正半轴于点
的正半轴于点![]() .点
.点![]() (其中
(其中![]() )是坐标平面内一个动点,且
)是坐标平面内一个动点,且![]() ,
,![]() 是以点
是以点![]() 为圆心,半径为2的圆,若
为圆心,半径为2的圆,若![]() 上的任意两个点都是
上的任意两个点都是![]() 的一对平衡点,直接写出
的一对平衡点,直接写出![]() 的取值范围.
的取值范围.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在传箴言活动中,某班团支部对该班全体团员在一个月内所发箴言条数的情况进行统计,并绘制成了如图所示的两幅统计图
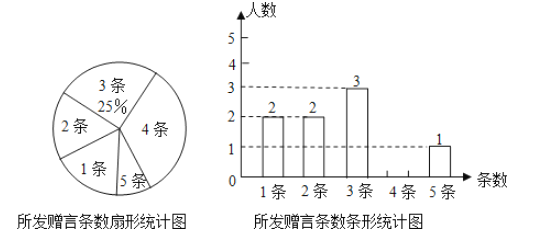
(1)将条形统计图补充完整;
(2)该班团员在这一个月内所发箴言的平均条数是________;
(3)如果发了3条箴言的同学中有两位男同学,发了4条箴言的同学中有三位女同学,现要从发了3条箴言和4条箴言的同学中分别选出一位参加总结会,请你用列表或树状图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,∠ABC=45°,AB=4![]() ,BC=9,直线MN平分平行四边形ABCD的面积,分别交边AD、BC于点M、N,若△BMN是以MN为腰的等腰三角形,则BN=_____.
,BC=9,直线MN平分平行四边形ABCD的面积,分别交边AD、BC于点M、N,若△BMN是以MN为腰的等腰三角形,则BN=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着社会的发展,私家车变得越来越普及,使用节能低油耗汽车,对环保有着非常积极的意义,某市有关部门对本市的某一型号的若干辆汽车,进行了一项油耗抽样实验:即在同一条件下,被抽样的该型号汽车,在油耗![]() 的情况下,所行驶的路程(单位:
的情况下,所行驶的路程(单位:![]() )进行统计分析,结果如图所示:
)进行统计分析,结果如图所示:
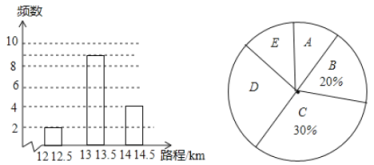
(注:记![]() 为
为![]() ,
,![]() 为
为![]() ,
,![]() 为
为![]() ,
,![]() 为
为![]() ,
,![]() 为
为![]() )
)
请依据统计结果回答以下问题:
(1)试求进行该试验的车辆数;
(2)请补全频数分布直方图;
查看答案和解析>>
科目:初中数学 来源: 题型:
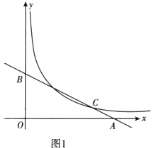
【题目】小明在课外研究中,设计如下题目:直线![]() 过点
过点![]() ,
,![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于点
交于点![]() .
.
(1)求直线和曲线的关系式.(图1)
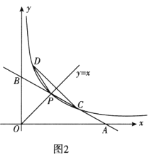
(2)小明发现曲线![]() 关于直线
关于直线![]() 对称,他把曲线
对称,他把曲线![]() 与直线
与直线![]() 的交点
的交点![]() 叫做曲线的顶点.(图2)
叫做曲线的顶点.(图2)
①直接写出![]() 点的坐标;
点的坐标;
②若点![]() 从
从![]() 点出发向上运动,运动到
点出发向上运动,运动到![]() 时停止,求此时
时停止,求此时![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com