
【题目】小明在课外研究中,设计如下题目:直线![]() 过点
过点![]() ,
,![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于点
交于点![]() .
.
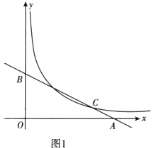
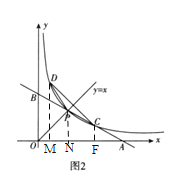
(1)求直线和曲线的关系式.(图1)
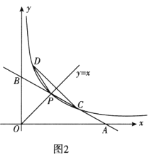
(2)小明发现曲线![]() 关于直线
关于直线![]() 对称,他把曲线
对称,他把曲线![]() 与直线
与直线![]() 的交点
的交点![]() 叫做曲线的顶点.(图2)
叫做曲线的顶点.(图2)
①直接写出![]() 点的坐标;
点的坐标;
②若点![]() 从
从![]() 点出发向上运动,运动到
点出发向上运动,运动到![]() 时停止,求此时
时停止,求此时![]() 的面积.
的面积.
【答案】(1)![]() ,
,![]() ;(2)①
;(2)①![]() ,②
,②![]() .
.
【解析】
(1)把![]() ,
,![]() 代入
代入![]() ,列出关于k和b的二元一次方程组,求出k和b的值,即可求出直线
,列出关于k和b的二元一次方程组,求出k和b的值,即可求出直线![]() 的解析式,把点
的解析式,把点![]() 代入直线解析式,求出n=1,把
代入直线解析式,求出n=1,把 ![]() 代入
代入![]() ,即可求出曲线的解析式.
,即可求出曲线的解析式.
(2)列方程组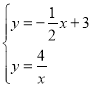 ,方程组的解,即为P点的坐标,由曲线
,方程组的解,即为P点的坐标,由曲线![]() 关于直线
关于直线![]() 对称,
对称,![]() ,可得点C和点D 关于
,可得点C和点D 关于![]() 对称,解点D的坐标,通过做辅助线,分别过点D、点P、点C向x轴作垂线,分别交x轴于点M、点N、点F,得到
对称,解点D的坐标,通过做辅助线,分别过点D、点P、点C向x轴作垂线,分别交x轴于点M、点N、点F,得到![]() ,求得
,求得![]() 的面积.
的面积.
(1)将点![]() ,
,![]() 的坐标代入
的坐标代入![]() ,
,
得:![]() ,解得
,解得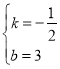
∴直线解析式为:![]() ,
,
∵直线![]() 过点
过点![]()
∴把C点坐标代入![]() 得,n=1,
得,n=1,
∴C点坐标为![]() ,
,
将C点坐标代入![]() ,解得m=4,
,解得m=4,
∴曲线的关系式为:![]() .
.
(2) ①∵点P是曲线![]() 与直线
与直线![]() 的交点,
的交点,
∴得到方程组![]() ,解得,
,解得,![]() 或
或![]() ,
,
∵x>0,
∴P点的坐标为![]()
②分别过点D、点P、点C向x轴作垂线,分别交x轴于点M、点N、点F.
∵曲线![]() 关于直线
关于直线![]() 对称,
对称,
∴当![]() 时,点C和点D 关于
时,点C和点D 关于![]() 对称,
对称,
∴点D得坐标为(1,4),
∴![]()
![]() ,
,
∴![]() .
.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:
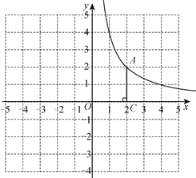
【题目】如图,在平面直角坐标系xOy中,函数![]() 的图象经过点
的图象经过点![]() ,作AC⊥x轴于点C.
,作AC⊥x轴于点C.
(1)求k的值;
(2)直线AB:![]() 图象经过点
图象经过点![]() 交x轴于点
交x轴于点![]() .横、纵坐标都是整数的点叫做整点.线段AB,AC,BC围成的区域(不含边界)为W.
.横、纵坐标都是整数的点叫做整点.线段AB,AC,BC围成的区域(不含边界)为W.
①直线AB经过![]() 时,直接写出区域W内的整点个数;
时,直接写出区域W内的整点个数;
②若区域W内恰有1个整点,结合函数图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年10月18日,党的十九大报告提出“乡村振兴”战略,之后各地发展乡村旅游,某村在2018年3月1日首次举办“百花节”,开园免费赏花,于是大批游客涌入该村赏花,吃农家饭买土特产,平均每人消费100元.
(1)据统计,某个周六早上开园后平均每小时有500人进园,两小时后,平均每小时有100人离园,园区规定,当园区内游客人数达到3000时,将停止进园,那么从开园起经过多少小时后停止进园?
(2)该村对园区加大建设和宣传力度,2019年3月1日,第二届“百花节”如期开园,同时规定进园门票费为每人60元,受各种因素影响,与2018年同期相比,人数在20000的基础上降低了a%,除门票外平均每人消费金额增长了![]() a%,园区总收入增长了
a%,园区总收入增长了![]() a%,求a的值.
a%,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
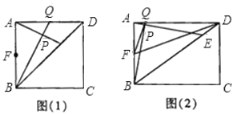
【题目】在四边形ABCD中,点E是对角线BD上一点,点Q是AD边上一点,BQ交AE于点P,∠ABQ=∠DAE,点F是AB边的中点.
(1)当四边形ABCD是正方形时,如图(1).
①若BE=BA,求证:△ABP≌△EBP;
②若BE=4DE,求证:AF2=AQ·AD.
(2)当四边形ABCD是矩形时,如图(2),连接FQ,FD.若BE=4DE,求证:∠AFQ=∠ADF.
查看答案和解析>>
科目:初中数学 来源: 题型:
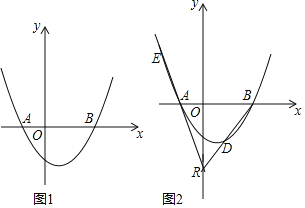
【题目】已知抛物线y=a(x2-cx-2c2)(a>0)交x轴于A、B两点(点A在点B的左侧),交y轴于点C.
(1) 取A(-1,0),则点B的坐标为___________;
(2) 若A(-1,0),a=1,点P为第一象限的抛物线,以P为圆心,![]() 为半径的圆恰好与AC相切,求P点坐标;
为半径的圆恰好与AC相切,求P点坐标;
(3) 如图,点R(0,n)在y轴负半轴上,直线RB交抛物线于另一点D,直线RA交抛物线于E.若DR=DB,EF⊥y轴于F,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数 y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线 x=1,下列结论:①ab<0;②b2>4ac;③a+b+2c<0;④3a+c<0. 其中正确的是( )
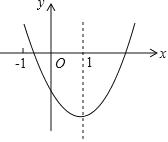
A.①④B.②④C.①②③D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 分别交y轴、x轴于A、B两点,抛物线y=﹣x2+bx+c过A、B两点.
分别交y轴、x轴于A、B两点,抛物线y=﹣x2+bx+c过A、B两点.
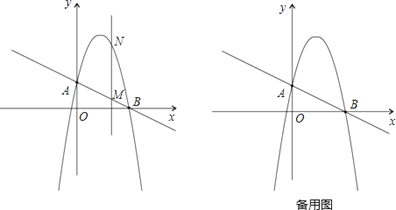
(1)求这个抛物线的解析式;
(2)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N.求当t取何值时,MN有最大值?最大值是多少?
(3)在(2)的情况下,以A、M、N、D为顶点作平行四边形,求第四个顶点D的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com