
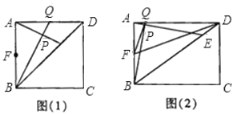
【题目】在四边形ABCD中,点E是对角线BD上一点,点Q是AD边上一点,BQ交AE于点P,∠ABQ=∠DAE,点F是AB边的中点.
(1)当四边形ABCD是正方形时,如图(1).
①若BE=BA,求证:△ABP≌△EBP;
②若BE=4DE,求证:AF2=AQ·AD.
(2)当四边形ABCD是矩形时,如图(2),连接FQ,FD.若BE=4DE,求证:∠AFQ=∠ADF.
【答案】(1)①证明见解析;②证明见解析;(2)证明见解析.
【解析】
(1)①由HL可证明Rt△ABP![]() Rt△EBP;
Rt△EBP;
②证明:过点E作EG⊥AD于点G可得△DEG∽△DBA,可得![]() ,以及△BAQ∽△AGE,可得
,以及△BAQ∽△AGE,可得![]() ,设DG=a,则GE=a,DA=5a,AB=5a,AG=4a.AQ=
,设DG=a,则GE=a,DA=5a,AB=5a,AG=4a.AQ=![]() ,代入即可证明:AF2=AQ·AD;
,代入即可证明:AF2=AQ·AD;
(2)延长AE交于CD边于点H,设DH=m,由AB∥CD,可得△DEH∽△BEA,可得AF=2m,由△BAQ∽△ADH,可得![]() 即AQ·DA=DH·AB=4m2=AF2,可证△AFQ∽△ADF,即可得出∠AFO=∠ADF.
即AQ·DA=DH·AB=4m2=AF2,可证△AFQ∽△ADF,即可得出∠AFO=∠ADF.
(1)①证明:在正方形ABCD中,∠ABQ=∠DAE.
∵∠ABQ+∠BAP=∠DAE+∠BAP=∠BAD=90°,
∴∠BPA=∠BPE=90°.
在Rt△ABP和Rt△EBP中,
![]() ,
,
∴Rt△ABP![]() Rt△EBP
Rt△EBP
②证明:过点E作EG⊥AD于点G,如图
∴∠GED=∠BAD=90°
∵∠GDE=∠ADB
∴△DEG∽△DBA,
∴![]()
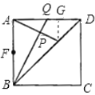
设DG=a,则GE=a,
∴DA=5a,AB=5a,AG=4a.
∵∠ABQ=∠DAE,∠BAQ=∠AGE,
∴△BAQ∽△AGE,
∴![]()
即AQ=![]()
∵F是AB边的中点,
∴![]()
又∵AQ·AD=![]() ,
,
∴AF2=AQ·AD
(2)证明:延长AE交于CD边于点H,设DH=m
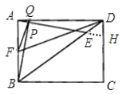
∵四边形ABCD是矩形,
∴AB∥CD,
∴△DEH∽△BEA,
∴![]() 即AB=4m,
即AB=4m,
∴AF=2m
∵∠BAQ=∠APB=90°
∴∠ABQ+∠BAP=∠DAH+∠BAP=90°
∴∠ABQ=∠DAH
∵∠BAQ=∠ADH=90°,∠ABQ=∠DAH
∴△BAQ∽△ADH,,
∴![]() 即AQ·DA=DH·AB=4m2=AF2,
即AQ·DA=DH·AB=4m2=AF2,
∴![]()
又∠FAO=∠DAF,
∴△AFQ∽△ADF,
∴∠AFO=∠ADF.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=![]() x2+mx+n与x轴相交于点A、B两点,过点B的直线y=x+b交抛物线于另一点C(-5,6),点D是线段BC上的一个动点(点D与点B、C不重合),作DE∥AC,交该抛物线于点E,
x2+mx+n与x轴相交于点A、B两点,过点B的直线y=x+b交抛物线于另一点C(-5,6),点D是线段BC上的一个动点(点D与点B、C不重合),作DE∥AC,交该抛物线于点E,
(1)求m,n,b的值;
(2)求tan∠ACB;
(3)探究在点D运动过程中,是否存在∠DEA=45°,若存在,则求此时线段AE的长;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
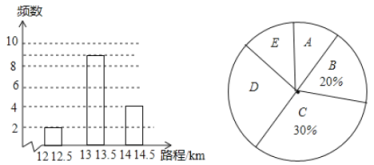
【题目】随着社会的发展,私家车变得越来越普及,使用节能低油耗汽车,对环保有着非常积极的意义,某市有关部门对本市的某一型号的若干辆汽车,进行了一项油耗抽样实验:即在同一条件下,被抽样的该型号汽车,在油耗![]() 的情况下,所行驶的路程(单位:
的情况下,所行驶的路程(单位:![]() )进行统计分析,结果如图所示:
)进行统计分析,结果如图所示:
(注:记![]() 为
为![]() ,
,![]() 为
为![]() ,
,![]() 为
为![]() ,
,![]() 为
为![]() ,
,![]() 为
为![]() )
)
请依据统计结果回答以下问题:
(1)试求进行该试验的车辆数;
(2)请补全频数分布直方图;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=10,BC=15,点D,E,P分别是边AC,AB;BC上的点,且AD=4,AE=4EB.若![]() 是等腰三角形,则CP的长是__________.
是等腰三角形,则CP的长是__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果抛物线C1的顶点在抛物线C2上,抛物线C2的顶点也在抛物线C1上,那么我们称抛物线C1与C2为“互相关联”的抛物线.如图,已知抛物线![]() 与
与![]() 是“互相关联”的抛物线,点A,B分别是抛物线C1,C2的顶点,抛物线C2经过点D(6,-1).
是“互相关联”的抛物线,点A,B分别是抛物线C1,C2的顶点,抛物线C2经过点D(6,-1).
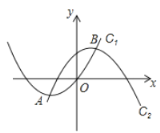
(1)直接写出点A,B的坐标和抛物线C2的解析式.
(2)抛物线C2上是否存在点E,使得△ABE是以AB为直角边的直角三角形?如果存在,请求出点E的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
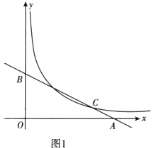
【题目】小明在课外研究中,设计如下题目:直线![]() 过点
过点![]() ,
,![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于点
交于点![]() .
.
(1)求直线和曲线的关系式.(图1)
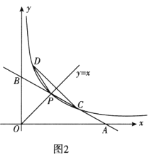
(2)小明发现曲线![]() 关于直线
关于直线![]() 对称,他把曲线
对称,他把曲线![]() 与直线
与直线![]() 的交点
的交点![]() 叫做曲线的顶点.(图2)
叫做曲线的顶点.(图2)
①直接写出![]() 点的坐标;
点的坐标;
②若点![]() 从
从![]() 点出发向上运动,运动到
点出发向上运动,运动到![]() 时停止,求此时
时停止,求此时![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
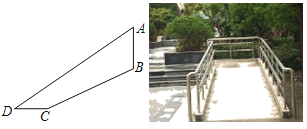
【题目】在商场里,为方便一部分残疾人出入,商场特意设计了一种特殊通道“无障碍通道”,如图,线段BC表示无障碍通道,线段AD表示普通扶梯,其中“无障碍通道”BC的坡度(或坡比)为i=1:2,BC=12![]() 米,CD=6米,∠D=30°,(其中点A、B、C、D均在同一平面内)则垂直升降电梯AB的高度约为( )米.
米,CD=6米,∠D=30°,(其中点A、B、C、D均在同一平面内)则垂直升降电梯AB的高度约为( )米.
A.10![]() B.10
B.10![]() ﹣12C.12D.10
﹣12C.12D.10![]() +12
+12
查看答案和解析>>
科目:初中数学 来源: 题型:
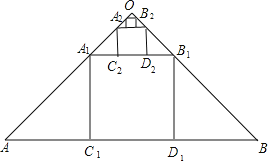
【题目】如图,在斜边长为1的等腰直角三角形OAB中,作内接正方形A1B1C1D1;在等腰直角三角形OA1B1中,作内接正方形A2B2C2D2;在等腰直角三角形OA2B2中,作内接正方形A3B3C3D3;……;依次作下去,则第n个正方形AnBnCnDn的边长是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com