
【题目】如果抛物线C1的顶点在抛物线C2上,抛物线C2的顶点也在抛物线C1上,那么我们称抛物线C1与C2为“互相关联”的抛物线.如图,已知抛物线![]() 与
与![]() 是“互相关联”的抛物线,点A,B分别是抛物线C1,C2的顶点,抛物线C2经过点D(6,-1).
是“互相关联”的抛物线,点A,B分别是抛物线C1,C2的顶点,抛物线C2经过点D(6,-1).
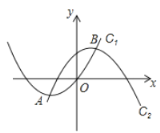
(1)直接写出点A,B的坐标和抛物线C2的解析式.
(2)抛物线C2上是否存在点E,使得△ABE是以AB为直角边的直角三角形?如果存在,请求出点E的坐标;如果不存在,请说明理由.
【答案】(1)A(-2,-1),B(2,3),![]() ;(2)存在,E的坐标为(6,-1)或(10,-13).
;(2)存在,E的坐标为(6,-1)或(10,-13).
【解析】
(1)由抛物线![]() 可得A(-2,-1),将
可得A(-2,-1),将![]() ,D(6,-1)代入C2:y2=ax2+x+c,求得y2=-
,D(6,-1)代入C2:y2=ax2+x+c,求得y2=-![]() x2+x+2,B(2,3).
x2+x+2,B(2,3).
(2)易得直线AB的解析式:![]() ,若B为直角顶点,
,若B为直角顶点,![]() ,E(6,-1);若A为直角顶点,
,E(6,-1);若A为直角顶点,![]() ,E(10,-13).
,E(10,-13).
(1)由抛物线![]() 可得
可得
A(-2,-1)
由抛物线C2:y2=ax2+x+c过点A,D(6,-1)
得![]()
解得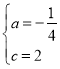
故抛物线C2的解析式为y2=-![]() x2+x+2.
x2+x+2.
∵y2=-![]() x2+x+2.
x2+x+2.
=![]() (x-2)2+3,
(x-2)2+3,
∴点B的坐标为(2,3).
(2)存在.
设点E的坐标为(m,![]() m2+m+2).
m2+m+2).
∵A(-2,-1),B(2,3),
∴AB2=(2+2)2+(3+1)2=32,
AE2=(m+2)2+(![]() m2+m+2+1)2,
m2+m+2+1)2,
BE2=(m-2)2+(m2+m+2-3)2.
①当点A为直角顶点时,有AB2+AE2=BE2,
即32+(m+2)2+(![]() m2+m+2+1)2
m2+m+2+1)2
=(m-2)2+(![]() m2+m+2-3)2,
m2+m+2-3)2,
解得m1=-2(不合题意,舍去),m2=10,
∴E(10,-13).
②当点B为直角顶点时,有AB2+BE2=AE2,
即32+(m-2)2+(![]() m2+m+2-3)2
m2+m+2-3)2
=(m+2)2+(![]() m2+m+2+1)2,
m2+m+2+1)2,
解得m3=6,m4=2(不合题意,舍去),
∴E(6,-1).
综上所述,当E的坐标为(6,-1)或(10,-13).


科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的点A,B点分别在x轴,y轴上,与双曲线y=![]() 恰好交于BC的中点E,若OB=2OA,则S△ABO的值为( )
恰好交于BC的中点E,若OB=2OA,则S△ABO的值为( )

A.6B.8C.12D.16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是矩形ABCD的边AB的中点,点F是边CD上一点,连接ED,EF,ED平分∠AEF,过点D作DG⊥EF于点M,交BC于点G,连接GE,GF,若FG∥DE,则![]() 的值是( )
的值是( )
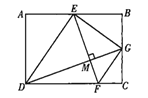
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,点E是对角线BD上一点,点Q是AD边上一点,BQ交AE于点P,∠ABQ=∠DAE,点F是AB边的中点.
(1)当四边形ABCD是正方形时,如图(1).
①若BE=BA,求证:△ABP≌△EBP;
②若BE=4DE,求证:AF2=AQ·AD.
(2)当四边形ABCD是矩形时,如图(2),连接FQ,FD.若BE=4DE,求证:∠AFQ=∠ADF.
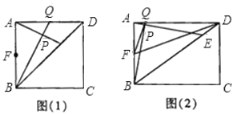
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】草莓是种老少皆宜的食品,深受市民欢迎.今年3月份,甲,乙两超市分别用3000元以相同的进价购进质量相同的草莓.甲超市销售方案是:将草莓按大小分类包装销售,其中大草莓400千克,以进价的2倍价格销售,剩下的小草莓以高于进价的10%销售.乙超市销售方案是:不将草莓按大小分类,直接包装销售,价格按甲超市大、小两种草莓售价的平均数定价.若两超市将草莓全部售完,其中甲超市获利2100元(其他成本不计).
(1)草莓进价为每千克多少元?
(2)乙超市获利多少元?并比较哪种销售方式更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
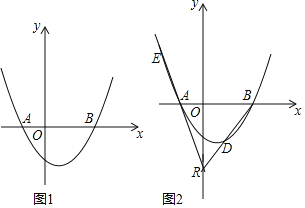
【题目】已知抛物线y=a(x2-cx-2c2)(a>0)交x轴于A、B两点(点A在点B的左侧),交y轴于点C.
(1) 取A(-1,0),则点B的坐标为___________;
(2) 若A(-1,0),a=1,点P为第一象限的抛物线,以P为圆心,![]() 为半径的圆恰好与AC相切,求P点坐标;
为半径的圆恰好与AC相切,求P点坐标;
(3) 如图,点R(0,n)在y轴负半轴上,直线RB交抛物线于另一点D,直线RA交抛物线于E.若DR=DB,EF⊥y轴于F,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】济南市地铁1号线于2019年1月1日起正式通车,在修建过程中,技术人员不断改进技术,提高工作效率,如在打通一条长600米的隧道时,计划用若干小时完成,在实际工作过程中,每小时打通隧道长度是原计划的1.2倍,结果提前2小时完成任务.
(1)求原计划每小时打通隧道多少米?
(2)如果按照这个速度下去,后面的300米需要多少小时打通?
查看答案和解析>>
科目:初中数学 来源: 题型:
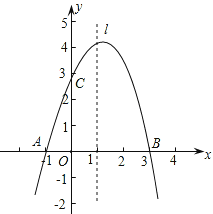
【题目】已知抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴.
(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,当△PAC的周长最小时,求点P的坐标;
(3)在直线l上是否存在点M,使△MAC为等腰三角形?若存在,直接写出所有符合条件的点M的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com