
【题目】已知抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴.
(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,当△PAC的周长最小时,求点P的坐标;
(3)在直线l上是否存在点M,使△MAC为等腰三角形?若存在,直接写出所有符合条件的点M的坐标;若不存在,请说明理由.
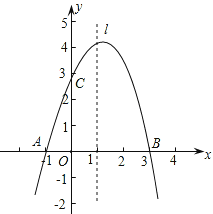
【答案】解:(1)∵A(-1,0)、B(3,0)经过抛物线y=ax2+bx+c,
∴可设抛物线为y=a(x+1)(x-3)。
又∵C(0,3) 经过抛物线,∴代入,得3=a(0+1)(0-3),即a=-1。
∴抛物线的解析式为y=-(x+1)(x-3),即y=-x2+2x+3。
(2)连接BC,直线BC与直线l的交点为P。 则此时的点P,使△PAC的周长最小。
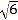
设直线BC的解析式为y=kx+b,
将B(3,0),C(0,3)代入,得:
![]() ,解得:
,解得:![]() 。
。
∴直线BC的函数关系式y=-x+3。
当x-1时,y=2,即P的坐标(1,2)。
(3)存在。点M的坐标为(1,![]() ),(1,-
),(1,-![]() ),(1,1),(1,0)。
),(1,1),(1,0)。
【解析】二次函数综合题,待定系数法,曲线上点的坐标与方程的关系,线段中垂线的性质,三角形三边关系,等腰三角形的性质。
(1)可设交点式,用待定系数法求出待定系数即可。
(2)由图知:A、B点关于抛物线的对称轴对称,那么根据抛物线的对称性以及两点之间线段最短可知:若连接BC,那么BC与直线l的交点即为符合条件的P点。
(3)由于△MAC的腰和底没有明确,因此要分三种情况来讨论:①MA=AC、②MA=MC、②AC=MC;可先设出M点的坐标,然后用M点纵坐标表示△MAC的三边长,再按上面的三种情况列式求解:
∵抛物线的对称轴为: x=1,∴设M(1,m)。
∵A(-1,0)、C(0,3),∴MA2=m2+4,MC2=m2-6m+10,AC2=10。
①若MA=MC,则MA2=MC2,得:m2+4=m2-6m+10,得:m=1。
②若MA=AC,则MA2=AC2,得:m2+4=10,得:m=±![]() 。
。
③若MC=AC,则MC2=AC2,得:m2-6m+10=10,得:m=0,m=6,
当m=6时,M、A、C三点共线,构不成三角形,不合题意,故舍去。
综上可知,符合条件的M点,且坐标为(1,![]() ),(1,-
),(1,-![]() ),(1,1),(1,0)。
),(1,1),(1,0)。


科目:初中数学 来源: 题型:
【题目】如图,已知:点A、B、C、D在⊙O上,AB=CD,下列结论:①∠AOC=∠BOD;②∠BOD=2∠BAD;③AC=BD;④∠CAB=∠BDC;⑤∠CAO+∠CDO=180°.其中正确的个数为( )
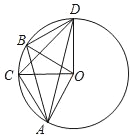
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,斜坡AB坡度为1:2.4,长度为52米,在坡顶B所在的平台上有一座高楼EF,已知在A处测得楼顶F的仰角为60°,在B处测得楼顶F的仰角为77°,则高楼EF的高度是( )(精确到米,参考数据:sin77°≈0.97,tan77°≈4.33,![]() ≈1.73)
≈1.73)
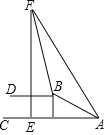
A. 125米 B. 105米 C. 85米 D. 65米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个长为4cm,宽为3cm的长方形木板在桌面上做无滑动的翻滚(顺时针方向),木板点A位置的变化为A→Al→A2,其中第二次翻滚被面上一小木块挡住,使木板与桌面成30°的角,则点A滚到A2位置时共走过的路径长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
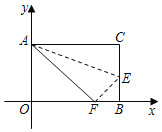
【题目】如图,长方形AOBC,以O为坐标原点,OB、OA分别在x轴、y轴上,点A的坐标为(0,8),点B的坐标为(10,0),点E是BC边上一点,把长方形AOBC沿AE翻折后,C点恰好落在x轴上点F处.
(1)求点E、F的坐标;
(2)求AF所在直线的函数关系式;
(3)在x轴上求一点P,使△PAF成为以AF为腰的等腰三角形,请直接写出所有符合条件的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地农民一直保持着冬种油菜的习惯,利用农闲冬种一季油菜该地农业部门对2017年的油菜籽的生产成本、市场价格、种植面积和产量等进行了统计,并绘制了如下的统计表与统计图(如图):

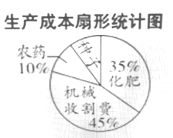
请根据以上信息解答下列问题:
(1)种植每亩油菜所需种子的成本是多少元?
(2)农民冬种油菜每亩获利多少元?
(3)2017年该地全县农民冬种油菜的总获利是多少元?(结果用科学记数法表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,将一个点(横坐标与纵坐标不相等)的横坐标与纵坐标互换后得到的点叫做这个点的“互换点”,如(-3,5)与(5,-3)是一对“互换点”。
(1)任意一对“互换点”________(填“都能”或“都不能”)在一个反比例函数的图象上;
(2)M、N是一对“互换点”,若点M的坐标为(2,-5),求直线MN的表达式;
(3)在抛物线![]() 的图象上有一对“互换点”A、B,其中点A在反比例函数
的图象上有一对“互换点”A、B,其中点A在反比例函数![]() 的图象上,直线AB经过点P(
的图象上,直线AB经过点P(![]() ,
,![]() ),求此抛物线的表达式.
),求此抛物线的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
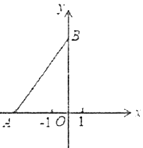
【题目】如图,在平面直角坐标系中,点![]() ,为
,为![]() 轴负半轴上一点,点
轴负半轴上一点,点![]() 为
为![]() 轴正半轴上一点,其中
轴正半轴上一点,其中![]() 满足方程
满足方程![]() .
.
(1)求点![]() 、
、![]() 的坐标;
的坐标;
(2)点![]() 为
为![]() 轴负半轴上一点,且
轴负半轴上一点,且![]() 的面积为
的面积为![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)在![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 的面积等于
的面积等于![]() 的面积的一半,若存在,求出相应的
的面积的一半,若存在,求出相应的![]() 点的坐标,若不存在,请说明理由.
点的坐标,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com