
【题目】如图,已知:点A、B、C、D在⊙O上,AB=CD,下列结论:①∠AOC=∠BOD;②∠BOD=2∠BAD;③AC=BD;④∠CAB=∠BDC;⑤∠CAO+∠CDO=180°.其中正确的个数为( )
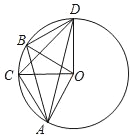
A. 2 B. 3 C. 4 D. 5
科目:初中数学 来源: 题型:
【题目】某超市准备购进甲、乙两种品牌的文具盒,甲、乙两种玩具盒的进价和售价如下表,预计购进乙品牌文具盒的数量y(个)与甲品牌玩具盒数量x(个)之间的函数关系如图所示.
甲 | 乙 | |
进价(元) | 15 | 30 |
售价(元) | 20 | 38 |
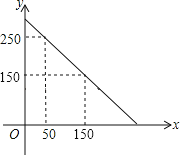
(1)y与x之间的函数关系式是 ;
(2)若超市准备用不超过6000元购进甲、乙两种文具盒,则至少购进多少个甲种文具盒?
(3)在(2)的条件下,写出销售所得的利润W(元)与x(个)之间的关系式,并求出获得的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在任意四边形ABCD中,M,N,P,Q分别是AB,BC,CD,DA上的点,对于四边形MNPQ的形状,以下结论中,错误的是![]()
![]()
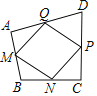
A. 当M,N,P,Q是各边中点,四边MNPQ一定为平行四边形
B. 当M,N,P,Q是各边中点,且![]() 时,四边形MNPQ为正方形
时,四边形MNPQ为正方形
C. 当M,N、P,Q是各边中点,且![]() 时,四边形MNPQ为菱形
时,四边形MNPQ为菱形
D. 当M,N、P、Q是各边中点,且![]() 时,四边形MNPQ为矩形
时,四边形MNPQ为矩形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E是AD上一点,连接BE,F为BE中点,且AF=BF,
(1)求证:四边形ABCD为矩形;
(2)过点F作FG⊥BE,垂足为F,交BC于点G,若BE=BC,S△BFG=5,CD=4,求CG.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=-![]() .
.
(1)将y=-![]() +x+
+x+![]() 用配方法化为y=a(x-h)2+k的形式;
用配方法化为y=a(x-h)2+k的形式;
(2)求该函数图象与两坐标轴交点的坐标;
(3)画出该函数的图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC的周长为18cm,BD为AC边上的中线,动点P,Q分别在线段BC,BD上运动,连接CQ,PQ,当BP长为_____cm时,线段CQ+PQ的和为最小.
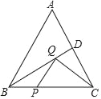
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴.
(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,当△PAC的周长最小时,求点P的坐标;
(3)在直线l上是否存在点M,使△MAC为等腰三角形?若存在,直接写出所有符合条件的点M的坐标;若不存在,请说明理由.
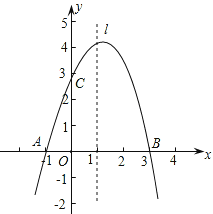
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com