练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知关于的二次函数和一次函数，若函数的图象始终在函数的图象的一侧，则常数的取值范围是__________．

    【答案】或

    【解析】

    若，则，根据根的判别式时，函数与的图象只有一个交点，此时或，对a的值进行分类讨论，结合图形，根据a的值对函数图形的影响，确定a的取值范围即可．

    解：若，则，整理得，

    当时，函数与的图象只有一个交点，此时或．

    ①当时，如图（1）所示．当从逐渐增大时，函数的图象开口向上，并随着的增大，开口越来越小，函数的图象逐渐向下平移，此时函数的图象在函数的图象上方．

    ②当时，如图（2）所示．当从逐渐减小时，函数的图象开口向下，并随着的减小，开口越来越小，函数的图象逐渐向上平移，此时函数的图象在函数的图象下方．

    综上所述，若函数的图象始终在函数的图象的一侧，的取值范围为或．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

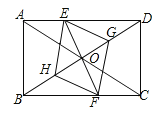
    【题目】已知：如图，在矩形ABCD中，点E在边AD上，点F在边BC上，且AE=CF，作EG∥FH，分别与对角线BD交于点G、H，连接EH，FG．

    （1）求证：△BFH≌△DEG；

    （2）连接DF，若BF=DF，则四边形EGFH是什么特殊四边形？证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

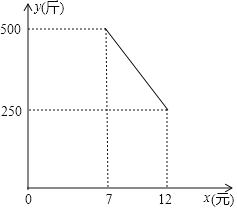
    【题目】某水果店每天的房租、人员工资等固定成本250元，水果进价是5元/斤，物价局规定售价不得高于12元/斤，也不得低于7元/斤，调查发现日均销量y（斤）与售价x（元）满足一次函数关系，图象如图．

    （1）求日均销量y（斤）与销售单价x（元）之间的函数关系式，并写出自变量取值范围；

    （2）设每天净利润为W元，那么定价多少时，可获得最大净利润？最大是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，正方形ABCD的点A，B点分别在x轴，y轴上，与双曲线y＝恰好交于BC的中点E，若OB＝2OA，则S△ABO的值为（ ）

    A.6B.8C.12D.16

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】2017年10月18日，党的十九大报告提出“乡村振兴”战略，之后各地发展乡村旅游，某村在2018年3月1日首次举办“百花节”，开园免费赏花，于是大批游客涌入该村赏花，吃农家饭买土特产，平均每人消费100元．

    （1）据统计，某个周六早上开园后平均每小时有500人进园，两小时后，平均每小时有100人离园，园区规定，当园区内游客人数达到3000时，将停止进园，那么从开园起经过多少小时后停止进园？

    （2）该村对园区加大建设和宣传力度，2019年3月1日，第二届“百花节”如期开园，同时规定进园门票费为每人60元，受各种因素影响，与2018年同期相比，人数在20000的基础上降低了a%，除门票外平均每人消费金额增长了a%，园区总收入增长了a%，求a的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

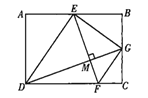
    【题目】如图，点E是矩形ABCD的边AB的中点，点F是边CD上一点，连接ED，EF，ED平分∠AEF，过点D作DG⊥EF于点M，交BC于点G，连接GE，GF，若FG∥DE，则 的值是(　　)

    A.B.C.D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

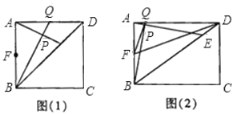
    【题目】在四边形ABCD中，点E是对角线BD上一点，点Q是AD边上一点，BQ交AE于点P，∠ABQ=∠DAE，点F是AB边的中点．

    （1）当四边形ABCD是正方形时，如图（1）．

    ①若BE=BA，求证：△ABP≌△EBP；

    ②若BE=4DE，求证：AF2=AQ·AD．

    （2）当四边形ABCD是矩形时，如图（2），连接FQ，FD．若BE=4DE，求证：∠AFQ=∠ADF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

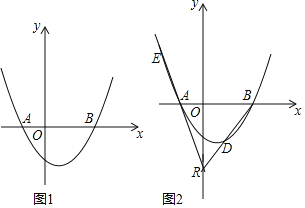
    【题目】已知抛物线y＝a（x2－cx－2c2）（a＞0）交x轴于A、B两点（点A在点B的左侧），交y轴于点C．

    （1） 取A（－1，0），则点B的坐标为___________；

    （2） 若A（－1，0），a＝1，点P为第一象限的抛物线，以P为圆心，为半径的圆恰好与AC相切，求P点坐标；

    （3） 如图，点R（0，n）在y轴负半轴上，直线RB交抛物线于另一点D，直线RA交抛物线于E．若DR＝DB，EF⊥y轴于F，求的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】△ABC中，BC=10，AB=，∠ABC=30°，点P在直线AC上，点P到直线AB的距离为1，则CP的长为_____．

    查看答案和解析>>

    同步练习册答案