
【题目】在商场里,为方便一部分残疾人出入,商场特意设计了一种特殊通道“无障碍通道”,如图,线段BC表示无障碍通道,线段AD表示普通扶梯,其中“无障碍通道”BC的坡度(或坡比)为i=1:2,BC=12![]() 米,CD=6米,∠D=30°,(其中点A、B、C、D均在同一平面内)则垂直升降电梯AB的高度约为( )米.
米,CD=6米,∠D=30°,(其中点A、B、C、D均在同一平面内)则垂直升降电梯AB的高度约为( )米.
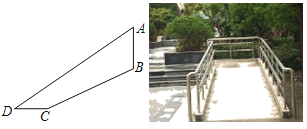
A.10![]() B.10
B.10![]() ﹣12C.12D.10
﹣12C.12D.10![]() +12
+12
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
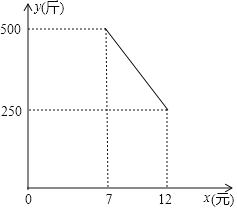
【题目】某水果店每天的房租、人员工资等固定成本250元,水果进价是5元/斤,物价局规定售价不得高于12元/斤,也不得低于7元/斤,调查发现日均销量y(斤)与售价x(元)满足一次函数关系,图象如图.
(1)求日均销量y(斤)与销售单价x(元)之间的函数关系式,并写出自变量取值范围;
(2)设每天净利润为W元,那么定价多少时,可获得最大净利润?最大是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
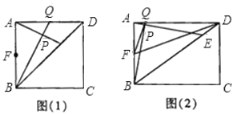
【题目】在四边形ABCD中,点E是对角线BD上一点,点Q是AD边上一点,BQ交AE于点P,∠ABQ=∠DAE,点F是AB边的中点.
(1)当四边形ABCD是正方形时,如图(1).
①若BE=BA,求证:△ABP≌△EBP;
②若BE=4DE,求证:AF2=AQ·AD.
(2)当四边形ABCD是矩形时,如图(2),连接FQ,FD.若BE=4DE,求证:∠AFQ=∠ADF.
查看答案和解析>>
科目:初中数学 来源: 题型:
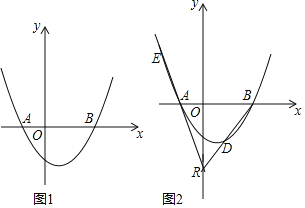
【题目】已知抛物线y=a(x2-cx-2c2)(a>0)交x轴于A、B两点(点A在点B的左侧),交y轴于点C.
(1) 取A(-1,0),则点B的坐标为___________;
(2) 若A(-1,0),a=1,点P为第一象限的抛物线,以P为圆心,![]() 为半径的圆恰好与AC相切,求P点坐标;
为半径的圆恰好与AC相切,求P点坐标;
(3) 如图,点R(0,n)在y轴负半轴上,直线RB交抛物线于另一点D,直线RA交抛物线于E.若DR=DB,EF⊥y轴于F,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】济南市地铁1号线于2019年1月1日起正式通车,在修建过程中,技术人员不断改进技术,提高工作效率,如在打通一条长600米的隧道时,计划用若干小时完成,在实际工作过程中,每小时打通隧道长度是原计划的1.2倍,结果提前2小时完成任务.
(1)求原计划每小时打通隧道多少米?
(2)如果按照这个速度下去,后面的300米需要多少小时打通?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数 y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线 x=1,下列结论:①ab<0;②b2>4ac;③a+b+2c<0;④3a+c<0. 其中正确的是( )
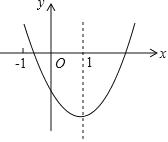
A.①④B.②④C.①②③D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,量角器的直径与直角三角板ABC的斜边AB重合,其中量角器零刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒4度的速度旋转,CP与量角器的半圆弧交于点E,第18秒时,点E在量角器上对应的读数是__________度.
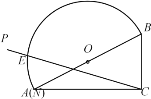
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com