
【题目】某公司推出一款产品,经市场调查发现,该产品的日销售量y(个)与销售单价x(元)之间满足一次函数关系,关于销售单价,日销售量,日销售利润的几组对应值如表:
销售单价x(元) | 85 | 95 | 105 | 115 |
日销售量y(个) | 175 | 125 | 75 | 25 |
日销售利润w(元) | 875 | 1875 | 1875 | 875 |
(注:日销售利润=日销售量×(销售单价﹣成本单价))
(1)求y与x的函数关系式;
(2)当销售单价x为多少元时,日销售利润w最大?最大利润是多少元?
(3)当销售单价x为多少元时,日销售利润w在1500元以上?(请直接写出x的范围)
【答案】(1)y=﹣5x+600;(2)当销售单价x为100元时,日销售利润w最大,最大利润是2000元;(3)当销售单价x在90元和110元之间时,日销售利润w在1500元以上.
【解析】
(1)根据题意和表格中的数据可以求得y关于x的函数解析式;
(2)根据题意可以列出相应的方程,从而可以求得生产成本和w的最大值;
(3)根据题意列不等式即可得到结论.
解:(1)设y关于x的函数解析式为y=kx+b,![]() ,得
,得![]() ,
,
即y关于x的函数解析式是y=﹣5x+600,
(2)设成本价为a元/个
当x=85时,875=175![]() (85-a),得a=80,
(85-a),得a=80,
根据题意得,w=(﹣5x+600)(x﹣80)=﹣5x2+1000x﹣48000=﹣5(x﹣100)2+2000,
∴当x=100时,w取得最大值,此时w=2000,
答:当销售单价x为100元时,日销售利润w最大,最大利润是2000元;
(3)根据题意得,﹣5(x﹣100)2+2000>1500,
解得90<x<110,
答:当销售单价x在90元和110元之间时,日销售利润w在1500元以上.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图1,正方形![]() 中, 点
中, 点![]() 是
是![]() 的中点,过点
的中点,过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 垂直
垂直![]() 的延长线于点
的延长线于点![]() ,交
,交![]() 于点
于点![]() .
.
(1)求证:![]() ;
;
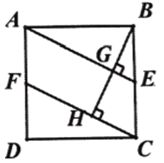
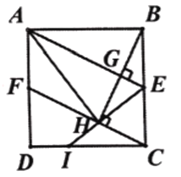
(2)如图2,连接![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点I,
于点I,
①求证:![]() ;
;
②求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
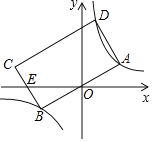
【题目】如图,矩形ABCD的顶点A,B,D分别落在双曲线y=![]() (k>0)的两个分支上,AB边经过原点O,CB边与x轴交于点E,且EC=EB,若点A的横坐标为1,则矩形ABCD的面积_____.
(k>0)的两个分支上,AB边经过原点O,CB边与x轴交于点E,且EC=EB,若点A的横坐标为1,则矩形ABCD的面积_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校团委举办了一次“中国梦,我的梦”演讲比赛,满分10分,学生得分均为整数,成绩达6分以上(含6分)为合格,达9分以上(含9分)为优秀.这次竞赛中甲,乙两组学生成绩分布的条形统计图如下:
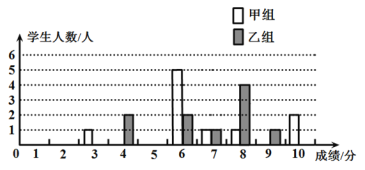
(1)将下表补充完整:
组别 | 平均分 | 中位数 | 众数 | 方差 | 合格率 | 优秀率 |
甲 | 6.8 |
| 6 | 3.96 | 90% | 20% |
乙 |
| 7.5 |
| 2.76 | 80% | 10% |
(2)小明同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上表可知,小明是 组学生(填“甲””或“乙”);
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你给出两条支持乙组同学观点的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校团委决定从4名学生会干部(小明、小华、小丽和小颖)中抽签确定2名同学去进行宣传活动,抽签规则:将4名同学姓名分别写在4张完全相同的卡片正面,把四张卡片背面朝上,洗匀后放在桌面上,既然从中随机抽取一张卡片,记下姓名,再从剩余的3张卡片中随机抽取第二张,记下姓名.试用画树状图或列表的方法表示这次抽签所有可能的结果,并求出小明被抽中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
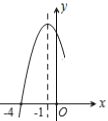
【题目】二次函数![]() 的部分图象如图所示,图象过点
的部分图象如图所示,图象过点![]() ,对称轴为直线
,对称轴为直线![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③一元二次方程
;③一元二次方程![]() 的解是
的解是![]() ,
,![]() ;④当
;④当![]() 时,
时,![]() ,其中正确的结论有__________.
,其中正确的结论有__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
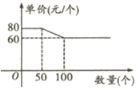
【题目】某批发部某一玩具价格如图所示,现有甲、乙两个商店,计划在“六一”儿童节前到该批发部购买此类玩具,两商店所需玩具总数为120个,乙商店所需数量不超过50个,设甲商店购买![]() 个,如果甲、乙两商店分别购买玩具,两商店需付款总和为
个,如果甲、乙两商店分别购买玩具,两商店需付款总和为![]() 元.
元.
(1)求![]() 关于
关于![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)若甲商店购买不超过100个,请说明甲、乙两商店联合购买比分别购买最多可节约多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
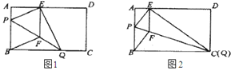
【题目】如图![]() ,在矩形纸片
,在矩形纸片![]() 中,
中,![]() ,
,![]() ,折叠纸片使
,折叠纸片使![]() 点落在边
点落在边![]() 上的
上的![]() 处,折痕为
处,折痕为![]() .过点
.过点![]() 作
作![]() 交
交![]() 于
于![]() ,连接
,连接![]() .
.
(1)求证:四边形![]() 为菱形;
为菱形;
(2)当点![]() 在
在![]() 边上移动时,折痕的端点
边上移动时,折痕的端点![]() ,
,![]() 也随之移动.
也随之移动.
①当点![]() 与点
与点![]() 重合时(如图
重合时(如图![]() ),求菱形
),求菱形![]() 的边长;
的边长;
②若限定![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上移动,求出点
上移动,求出点![]() 在边
在边![]() 上移动的最大距离.
上移动的最大距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
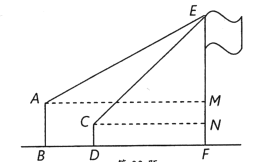
【题目】如图,某数学兴趣小组在活动课上测量学校旗杆的高度.已知小亮站着测量,眼睛与地面的距离(AB)是1.6米,看旗杆顶部E的仰角为30°;小敏蹲着测量,眼睛与地面的距离(CD)是0.6米,看旗杆顶部E的仰角为45°.两人相距5米且位于旗杆同侧(点B、D、F在同一直线上).求旗杆EF的高度.(结果保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com