
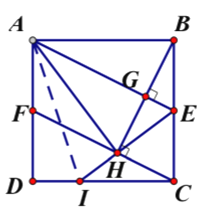
【题目】如图1,正方形![]() 中, 点
中, 点![]() 是
是![]() 的中点,过点
的中点,过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 垂直
垂直![]() 的延长线于点
的延长线于点![]() ,交
,交![]() 于点
于点![]() .
.
(1)求证:![]() ;
;
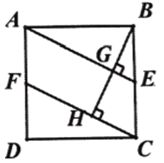
(2)如图2,连接![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点I,
于点I,
①求证:![]() ;
;
②求![]() 的值.
的值.
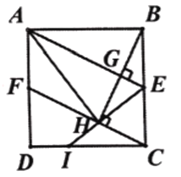
【答案】(1)证明见解析;(2)①证明见解析;②![]()
【解析】
(1)根据正方形的性质与已知条件证明![]() ,利用AAS证明
,利用AAS证明![]() ;
;
(2)①结合(1)证明![]() ,根据相似三角形的性质进行求证;
,根据相似三角形的性质进行求证;
②方法一:延长![]() 和
和![]() 交于点
交于点![]() ,由正方形的性质与已知条件得出四边形
,由正方形的性质与已知条件得出四边形![]() 是平行四边形,
是平行四边形,![]() ,
,![]() ,由①得出
,由①得出![]() ,进而可求出
,进而可求出![]() ,最后根据相似三角形的性质进行求解;
,最后根据相似三角形的性质进行求解;
方法二:连接![]() ,利用直角三角形斜边上的中线为斜边的一半得出
,利用直角三角形斜边上的中线为斜边的一半得出![]() ,进而证明
,进而证明![]() ,
,![]() ,根据全等三角形的性质得出
,根据全等三角形的性质得出![]() ,设
,设![]() ,
,![]() , 在
, 在![]() 中利用勾股定理求出x,进而求解.
中利用勾股定理求出x,进而求解.
解:(1)证明:![]() 四边形
四边形![]() 是正方形,
是正方形,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() 的延长线于点
的延长线于点![]() ,交
,交![]() 于点
于点![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() (AAS);
(AAS);
(2)①证明:![]() ,
,
又![]() ,
,
即![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
②方法一:如图,延长![]() 和
和![]() 交于点
交于点![]() ,
,
![]() ,
,![]() 的延长线于点
的延长线于点![]() ,交
,交![]() 于点
于点![]() ,
,
![]() ,
,
![]() 四边形
四边形![]() 是正方形,
是正方形,
![]() ,
,
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,![]() ,
,![]() ,
,
![]() ,
,
![]() 点
点![]() 是
是![]() 中点,
中点,
在![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,
![]() 点
点![]() 是
是![]() 中点,
中点,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
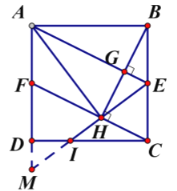
方法二:如图, 连接![]() ,
,
![]() 点
点![]() 是
是![]() 中点,
中点,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
在![]() 中,由勾股定理得,
中,由勾股定理得,![]()
解得,![]() ,
,
![]() ,
,
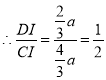 .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
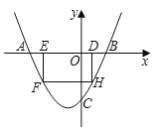
【题目】如图,抛物线![]() 与 x 轴交于点 A、B,与 y 轴交于点 C,且 OC=2OB, 点 D 为线段 OB 上一动点(不与点 B 重合),过点 D 作矩形 DEFH,点 H、F 在抛物线上,点 E 在 x 轴 上.
与 x 轴交于点 A、B,与 y 轴交于点 C,且 OC=2OB, 点 D 为线段 OB 上一动点(不与点 B 重合),过点 D 作矩形 DEFH,点 H、F 在抛物线上,点 E 在 x 轴 上.
(1)求抛物线的解析式;
(2)当矩形 DEFH 的周长最大时,求矩形 DEFH 的面积;
(3)在(2)的条件下,矩形 DEFH 不动,将抛物线沿着 x 轴向左平移 m 个单位,抛物线与矩形 DEFH的边交于点 M、N,连接 M、N.若 MN 恰好平分矩形 DEFH 的面积,求 m 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
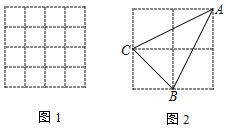
【题目】如图1,每个小正方形的边长都为1,点A、B、C在正方形网格的格点上,AB=5,AC=2,BC=![]() .
.
(1)请在网格中画出△ABC
(2)如图2,直接写出:
①AC= ,BC= .
②△ABC的面积为 .
③AB边上的高为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=x2+2ax-3与x轴交于A、B(1,0)两点(点A在点B的左侧),与y轴交于点C,将抛物线沿y轴平移m(m>0)个单位,当平移后的抛物线与线段OA有且只有一个交点时,则m的取值范围是_______________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是小安填写的数学实践活动报告的部分内容
题 目 | 测量铁塔顶端到地面的高度 | |
测量目标示意图 |
|
|
相关数据 | CD=20m,ɑ=45°,β=52° | |
求铁塔的高度FE(结果精确到1米)(参考数据:sin52°≈0.79, cos52°≈0.62,tan52°≈1.28)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】题目:为了美化环境,某地政府计划对辖区内![]() 的土地进行绿化.为了尽快完成任务,实际平均每月的绿化面积是原计划的1.5倍,结果提前2个月完成任务.求原计划平均每月的绿化面积.
的土地进行绿化.为了尽快完成任务,实际平均每月的绿化面积是原计划的1.5倍,结果提前2个月完成任务.求原计划平均每月的绿化面积.
甲同学所列的方程为![]()
乙同学所列的方程为![]()
(1)甲同学所列的方程中![]() 表示 .乙同学所列的方程中
表示 .乙同学所列的方程中![]() 表示 .
表示 .
(2)任选甲、乙两同学的其中一个方法解答这个题目.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与直线
两点,与直线![]() 交于
交于![]() 、
、![]() 两点,直线
两点,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
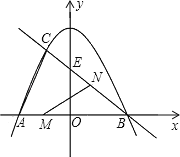
(1)求直线![]() 的解析式:
的解析式:
(2)若点![]() 在线段
在线段![]() 上以每秒1个单位长度的速度从点
上以每秒1个单位长度的速度从点![]() 向点
向点![]() 运动(不与点
运动(不与点![]() 、
、![]() 重合),同时,点
重合),同时,点![]() 在射线
在射线![]() 上以每秒2个单位长度的速度从点
上以每秒2个单位长度的速度从点![]() 向点
向点![]() 方向运动,设运动的时间为
方向运动,设运动的时间为![]() 秒,
秒,![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的函数关系式,并求
的函数关系式,并求![]() 取何值时,
取何值时,![]() 最大?最大值是多少?
最大?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司推出一款产品,经市场调查发现,该产品的日销售量y(个)与销售单价x(元)之间满足一次函数关系,关于销售单价,日销售量,日销售利润的几组对应值如表:
销售单价x(元) | 85 | 95 | 105 | 115 |
日销售量y(个) | 175 | 125 | 75 | 25 |
日销售利润w(元) | 875 | 1875 | 1875 | 875 |
(注:日销售利润=日销售量×(销售单价﹣成本单价))
(1)求y与x的函数关系式;
(2)当销售单价x为多少元时,日销售利润w最大?最大利润是多少元?
(3)当销售单价x为多少元时,日销售利润w在1500元以上?(请直接写出x的范围)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com