
【题目】下表是小安填写的数学实践活动报告的部分内容
题 目 | 测量铁塔顶端到地面的高度 | |
测量目标示意图 |
|
|
相关数据 | CD=20m,ɑ=45°,β=52° | |
求铁塔的高度FE(结果精确到1米)(参考数据:sin52°≈0.79, cos52°≈0.62,tan52°≈1.28)
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() 是
是![]() 延长线上的定点,
延长线上的定点,![]() 为
为![]() 边上的一个动点,连接
边上的一个动点,连接![]() ,将射线
,将射线![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,交射线
,交射线![]() 于点
于点![]() ,连接
,连接![]() .
.
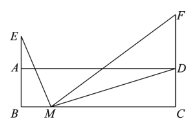
小东根据学习函数的经验,对线段![]() 的长度之间的关系进行了探究.
的长度之间的关系进行了探究.
下面是小东探究的过程,请补充完整:
(1)对于点![]() 在
在![]() 上的不同位置,画图、测量,得到了线段
上的不同位置,画图、测量,得到了线段![]() 的长度的几组值,如下表:
的长度的几组值,如下表:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | 位置8 | 位置9 | |
| 0.00 | 0.53 | 1.00 | 1.69 | 2.17 | 2.96 | 3.46 | 3.79 | 4.00 |
| 0.00 | 1.00 | 1.74 | 2.49 | 2.69 | 2.21 | 1.14 | 0.00 | 1.00 |
| 4.12 | 3.61 | 3.16 | 2.52 | 2.09 | 1.44 | 1.14 | 1.02 | 1.00 |
在![]() 的长度这三个量中,确定_____的长度是自变量,_____的长度和_____的长度都是这个自变量的函数;
的长度这三个量中,确定_____的长度是自变量,_____的长度和_____的长度都是这个自变量的函数;
(2)在同一平面直角坐标系![]() 中,画出(1)中所确定的两个函数的图象;
中,画出(1)中所确定的两个函数的图象;
(3)结合画出的函数图象,解决问题:当![]() 时,
时,![]() 的长度约为________
的长度约为________![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,函数![]() 的图象经过点
的图象经过点![]() ,作AC⊥x轴于点C.
,作AC⊥x轴于点C.
(1)求k的值;
(2)直线AB:![]() 图象经过点
图象经过点![]() 交x轴于点
交x轴于点![]() .横、纵坐标都是整数的点叫做整点.线段AB,AC,BC围成的区域(不含边界)为W.
.横、纵坐标都是整数的点叫做整点.线段AB,AC,BC围成的区域(不含边界)为W.
①直线AB经过![]() 时,直接写出区域W内的整点个数;
时,直接写出区域W内的整点个数;
②若区域W内恰有1个整点,结合函数图象,求a的取值范围.
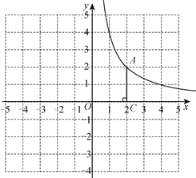
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D、E分别是△ABC的边AB、AC的中点,H、G是边BC上的点,且HG=![]() BC,S△ABC =12,则图中阴影部分的面积为( )
BC,S△ABC =12,则图中阴影部分的面积为( )
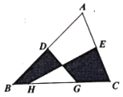
A.6B.4C.3D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
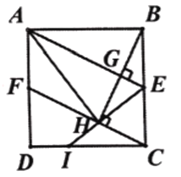
【题目】如图1,正方形![]() 中, 点
中, 点![]() 是
是![]() 的中点,过点
的中点,过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 垂直
垂直![]() 的延长线于点
的延长线于点![]() ,交
,交![]() 于点
于点![]() .
.
(1)求证:![]() ;
;
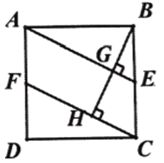
(2)如图2,连接![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点I,
于点I,
①求证:![]() ;
;
②求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
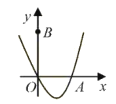
【题目】如图,在平面直角坐标系中,![]() 为坐标原点.抛物线
为坐标原点.抛物线![]() 与
与![]() 轴正半轴交于点
轴正半轴交于点![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,![]() 是该抛物线第一象限图像上的一点,
是该抛物线第一象限图像上的一点,![]() 三点均在某一个正方形的边上,且该正方形的任何一条边均与某条坐标轴平行,设点
三点均在某一个正方形的边上,且该正方形的任何一条边均与某条坐标轴平行,设点![]() 的横坐标为
的横坐标为![]() .若这个正方形的面积最小,则
.若这个正方形的面积最小,则![]() 的取值范围是__________.
的取值范围是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在平面直角坐标系中,![]() 为坐标原点,
为坐标原点,![]() 的边
的边![]() 平行于
平行于![]() 轴.若
轴.若![]() 的三个顶点都在二次函数
的三个顶点都在二次函数![]() 的图像上,则称
的图像上,则称![]() 为该二次函数图像的“伴随三角形”.
为该二次函数图像的“伴随三角形”.![]() 为抛物
为抛物![]() 的“伴随三角形”.
的“伴随三角形”.
(1)若点![]() 是抛物线与
是抛物线与![]() 轴的交点,求点
轴的交点,求点![]() 的坐标.
的坐标.
(2)若点![]() 在该抛物线的对称轴上,且到边
在该抛物线的对称轴上,且到边![]() 的距离为2,求
的距离为2,求![]() 的面积.
的面积.
(3)设![]() 两点的坐标分别为
两点的坐标分别为![]() ,比较
,比较![]() 与
与![]() 的大小,并求
的大小,并求![]() 的取值范围.
的取值范围.
(4)![]() 是抛物线
是抛物线![]() 的“伴随三角形”,点
的“伴随三角形”,点![]() 在点
在点![]() 的左侧,且
的左侧,且![]() ,点
,点![]() 的横坐标是点
的横坐标是点![]() 的横坐标的2倍,设该抛物线在
的横坐标的2倍,设该抛物线在![]() 上最高点的纵坐标为
上最高点的纵坐标为![]() ,当
,当![]() 时,直接写出
时,直接写出![]() 的取值范围和
的取值范围和![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学老师为了了解学生在数学学习中常见错误的纠正情况,收集整理了学生在作业和考试中的常见错误,编制了10道选择题,每题3分,对他所教的初三(1)班、(2)班进行了检测,如图表示从两班各随机抽取的10名学生的得分情况.
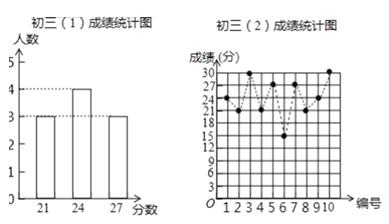
(1)利用图中提供的信息,补全下表:
班级 | 平均数/分 | 中位数/分 | 众数/分 | 方差/分 |
初三(1)班 | 24 | 24 | ________ | 5.4 |
初三(2)班 | 24 | _________ | 21 | ________ |
(2)哪个班的学生纠错的得分更稳定?若把24分以上(含24分)记为“优秀”,两班各40名学生,请估计两班各有多少名学生成绩优秀;
(3)现从两个班抽取了数学成绩最好的甲、乙、丙、丁四位同学,并随机分成两组进行数学竞赛,求恰好选中甲、乙一组的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
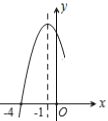
【题目】二次函数![]() 的部分图象如图所示,图象过点
的部分图象如图所示,图象过点![]() ,对称轴为直线
,对称轴为直线![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③一元二次方程
;③一元二次方程![]() 的解是
的解是![]() ,
,![]() ;④当
;④当![]() 时,
时,![]() ,其中正确的结论有__________.
,其中正确的结论有__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com