
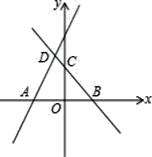
【题目】直线y=2x+m(m>0)与x轴交于点A(﹣2,0),直线y=﹣x+n(n>0)与x轴、y轴分别交于B、C两点,并与直线y=2x+m(m>0)相交于点D,若AB=4.
(1)求点D的坐标;
(2)求出四边形AOCD的面积;
(3)若点P为x轴上一动点,且使PD+PC的值最小,不写过程,直接写出点P的坐标。
【答案】(1)D点坐标为(﹣![]() ,
, ![]() );
);
(2)四边形AOCD的面积=![]() ;
;
(3)点E的坐标为(2![]() ﹣2,0)、(﹣2
﹣2,0)、(﹣2![]() ﹣2,0)、(2,0)、(0,0).
﹣2,0)、(2,0)、(0,0).
【解析】试题分析:(1)先把A点坐标代入y=2x+m得到m=4,则y=-2x+4,再利用AB=4可得到B点坐标为(2,0),则把B点坐标代入y=-x+n可得到n=2,则y=-x+2,然后根据两直线相交的问题,通过解方程组![]() 得到D点坐标;
得到D点坐标;
(2)先确定C点坐标为(0,2),然后利用四边形AOCD的面积=S△DAB-S△COB进行计算即可;(3)先利用A、C两点的坐标特征得到△ACO为等腰直角三角形,AC=![]() ,然后分类讨论:当AE=AC=
,然后分类讨论:当AE=AC=![]() 时,以A点为圆心,2
时,以A点为圆心,2![]() 画弧交x轴于E1点和E2点,再写出它们的坐标;当CE=CA时,E3点与点A关于y轴对称,即可得到它的坐标;当EA=EC时,E4点为坐标原点.
画弧交x轴于E1点和E2点,再写出它们的坐标;当CE=CA时,E3点与点A关于y轴对称,即可得到它的坐标;当EA=EC时,E4点为坐标原点.
试题解析:(1)把A(﹣2,0)代入y=2x+m得﹣4+m=0,
解得m=4,
∴y=﹣2x+4,
∵AB=4,A(﹣2,0),
∴B点坐标为(2,0),
把B(2,0)代入y=﹣x+n得﹣2+n=0,
解得n=2,
∴y=﹣x+2,
解方程组![]() 得
得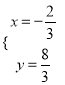 ,
,
∴D点坐标为(﹣![]() ,
, ![]() );
);
(2)当x=0时,y=﹣x+2=2,
∴C点坐标为(0,2),
∴四边形AOCD的面积=S△DAB﹣S△COB=![]() ×4×
×4×![]() ﹣
﹣![]() ×2×2=
×2×2=![]() ;
;
(3)∵A(﹣2,0),C(0,2),
∴AC=![]() ,
,
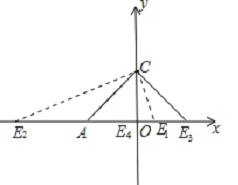
当AE=AC=![]() 时,E1点的坐标为(
时,E1点的坐标为(![]() ﹣2,0),E2点的坐标为(﹣
﹣2,0),E2点的坐标为(﹣![]() ﹣2,0);
﹣2,0);
当CE=CA时,E3点的坐标为(2,0),
当EA=EC时,E4点的坐标为(0,0),
综上所述,点E的坐标为(![]() ﹣2,0)、(﹣
﹣2,0)、(﹣![]() ﹣2,0)、(2,0)、(0,0).
﹣2,0)、(2,0)、(0,0).


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
【题目】2018年,宜宾市有5481000人口,将5481000用科学计数法(保留两个有效数字)表示为( )
A. 54×105 B. 0.55×106 C. 5.5×106 D. 5.4×106
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列频数分布表考查50名学生年龄时,这些学生的年龄落在5个小组中,第一、二、三、五组的数据个数分别是1,9,15,5,则第四组的频数是( ).
A. 10 B. 9 C. 15 D. 20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知箭头的方向是水流的方向,一艘游艇从江心岛的右侧A点逆流航行3小时到达B点后,又继续顺流航行2小时15分钟到达C点,总共行驶了198 km,已知游艇在静水中的速度是38 km/h.

(1)求水流的速度;
(2)由于AC段在建桥,游艇用同样的速度沿原路返回共需要多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
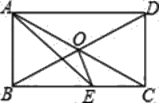
【题目】如图,在矩形ABCD中,∠BAD的平分线交BC于点E,O为对角线AC、BD的交点,且∠CAE=15° .
(1)求证:△AOB为等边三角形;
(2)求∠BOE度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
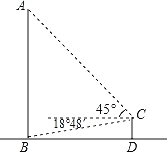
【题目】(2016湖北省荆州市第15题)全球最大的关公塑像矗立在荆州古城东门外.如图,张三同学在东门城墙上C处测得塑像底部B处的俯角为18°48′,测得塑像顶部A处的仰角为45°,点D在观测点C正下方城墙底的地面上,若CD=10米,则此塑像的高AB约为 米(参考数据:tan78°12′≈4.8).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com