
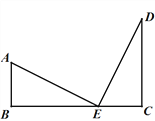
【题目】如图E在BC上,AB⊥BC于B,DC⊥BC于C,连结AE、DE,AE=DE.若AB=20,DC=40,BC=60.
(1)求DE的长
(2)求∠AED的度数
【答案】(1)20![]() (2)∠AED=90°
(2)∠AED=90°
【解析】试题分析:(1)设BE=x,利用勾股定理表示出AE2、DE2,然后根据AE=DE列出方程求出x,再由勾股定理即可得出结论:
(2)再利用“HL”证明Rt△ABE和Rt△EDC全等根据全等三角形对应角相等可得∠AEB=∠D,再根据平角等于180°列式计算即可求出∠AED=90°.
试题解析:解:(1)∵AB⊥BC,CD⊥BC,∴∠ABC=∠DCB=90°,设BE=x,在Rt△ABE和Rt△DCE中,根据勾股定理得,AB2+BE2=AE2,DC2+CE2=DE2,∵AE=DE,∴AB2+BE2=DC2+CE2,∴202+x2=(60-x)2+402,解得x=40,即DE=![]() =
=![]() =
=![]() ;
;
(2)在Rt△ABE和Rt△DCE中,∵AE=DE,BE=CD=40,∴Rt△ABE≌Rt△DCE(HL),∴∠AEB=∠D,∵∠CED+∠D=90°,∴∠CED+∠AEB=90°,∴∠AED=180°﹣∠CED﹣∠AEB=180°﹣90°=90°.


科目:初中数学 来源: 题型:
【题目】计算:
(1)﹣20+(﹣14)﹣(﹣18)﹣13
(2)﹣4÷ ![]() ﹣(﹣
﹣(﹣ ![]() )×(﹣30)
)×(﹣30)
(3)﹣22+|5﹣8|+24÷(﹣3)× ![]()
(4)( ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() )×24÷(﹣2)3 .
)×24÷(﹣2)3 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点(﹣1,y1),(1,y2)都在直线y=﹣3x+2上,则y1,y2的值的大小关系是( )
A. y1<y2 B. y2<y1 C. y1=y2 D. 无法判断
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. “367人中必有2人的生日是同一天”是必然事件
B. 了解一批灯泡的使用寿命采用全面调查
C. 一组数据6,5,3,5,4的众数是5,中位数是3
D. 一组数据10,11,12,9,8的平均数是10,方差是1.5
查看答案和解析>>
科目:初中数学 来源: 题型:
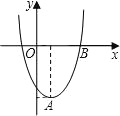
【题目】在直角坐标平面内,二次函数图象的顶点为A(1,﹣4),且过点B(3,0).
(1)求该二次函数的解析式;
(2)将该二次函数图象向右平移几个单位,可使平移后所得图象经过坐标原点?并直接写出平移后所得图象与x轴的另一个交点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个点从数轴上的原点开始,先向右移动3个单位长度,再向左移动5个单位长度,可以看到终点表示的数是﹣2.
已知点A是数轴上的点,完成下列各题:![]()
(1)如果点A表示的数是3,将点A先向左移动7个单位长度,再向右移动5个单位长度,那么终点B表示的数是 , A、B两点间的距离为;
(2)如果点A表示的数是﹣4,将点A先向右移动168个单位长度,再向左移动256个单位长度,那么终点B表示的数是 , A、B两点间的距离为;
一般地,如果点A表示的数是m,将点A先向右移动n个单位长度,再向左移动t个单位长度,那么终点B表示的数是 , A、B两点间的距离为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com