
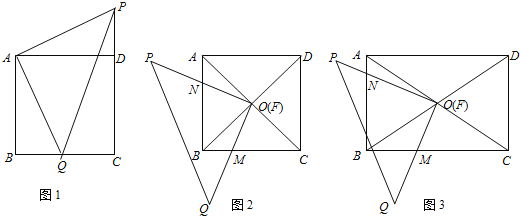
【题目】(1)正方形ABCD与等腰直角三角形PAQ如图1所示重叠在一起,其中∠PAQ=90°,点Q在BC上,连接PD,△ADP与△ABQ全等吗?请说明理由.
(2)如图2,O为正方形ABCD对角线的交点,将一直角三角板FPQ的直角顶点F与点O重合转动三角板使两直角边始终与BC、AB相交于点M、N,使探索OM与ON的数量关系,并说明理由.
(3)如图3,将(2)中的“正方形”改成“长方形”,其它的条件不变,且AB=4,AD=6,FM=x,FN=y,试求y与x之间的函数关系式.
【答案】(1)△ADP≌△ABQ,理由见解析;
(2)AC⊥BD,理由见解析;
(3)y与x之间的函数关系式为: ![]() .
.
【解析】试题分析:(1)根据正方形的性质和等腰直角三角形的性质就可以求得△ADP与△ABQ全等;
(2)根据正方形的性质和等腰直角三角形的性质就可以得△ANO≌△BMO,从而得出ON=OM;
(3)过点O作OE⊥AB于E,OH⊥BC于H,由条件求出OE、OH的值,再通过证明△OEN∽△OHM,利用相似三角形的性质就可以求出结论.
试题解析:(1)△ADP≌△ABQ.
理由:如图1,∵四边形ABCD是正方形,
∴AB=AD,∠B=∠ADP=∠BAD=90°
∵△PAQ是等腰直角三角形,
∴AQ=AP.
∵∠PAQ=90°,
∴∠BAD=∠PAQ,
∴∠BAD-∠QAD=∠PAQ-∠QAD,
∴∠BAQ=∠PAD.
∵在△ADP和△ABQ中,
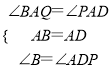
∴△ADP≌△ABQ(ASA);
(2)OM=ON.
理由:如图2,∵四边形ABCD是正方形,
∴AO=BO,∠AOB=90°,∠OAB=∠OBC=45°.
∴∠AOB=∠POQ,
∴∠AOB-∠NOB=∠POQ-∠NOB,
∴∠AON=∠BOM
∵在△AON和△BOM中,
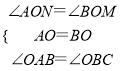 ,
,
∴△AON≌△BOM(ASA)
∴OM=ON;
(3)如图4,
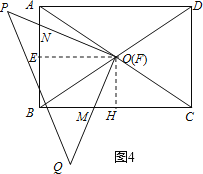
过点O作OE⊥AB于E,OH⊥BC于H,
∴∠OEN=∠OHM=90°,OE=![]() AD,OH=
AD,OH=![]() AB.
AB.
∵AB=4,AD=6,
∴OE=3,OH=2.
∵∠ABC=90°,
∴四边形EBHO是矩形,
∴∠EOH=90°,
∴∠EOH=∠POQ,
∴∠EOH-∠EOM=∠POQ-∠EOM,
∴∠EON=∠HOM.
∴△OEN∽△OHM,
∴![]() ,
,
即![]()
∴y= ![]() .
.


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】下列事件中,随机事件是( )
A.任意画一个三角形,其内角和为180°B.经过有交通信号的路口,遇到红灯
C.在只装了红球的袋子中摸到白球D.太阳从东方升起
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E、F是四边形ABCD的对角线BD上的两点,BF=DE,AE=CF,∠1=∠2. 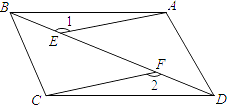
(1)求证:△ABE≌△CDF;
(2)四边形ABCD是平行四边形吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是矩形,延长AB至点F,连结CF,使得CF=AF,过点A作AE⊥FC于点E.
(1)求证:AD=AE.
(2)连结CA,若∠DCA=70°,求∠CAE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图中显示了10名同学平均每周用于阅读课外书的时间和用于看电视的时间(单位:小时)。
(1)用有序实数对表示图中各点。
(2)图中有一个点位于方格的对角线上,这表示什么意思?
(3)图中方格纸的对角线的左上方的点有什么共同的特点?它右下方的点呢?
(4)估计一下你每周用于阅读课外书的时间和用于看电视的时间,在图上描出来,这个点位于什么位置?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com