
【题目】如图,E、F是四边形ABCD的对角线BD上的两点,BF=DE,AE=CF,∠1=∠2. 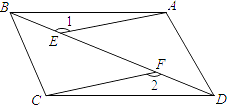
(1)求证:△ABE≌△CDF;
(2)四边形ABCD是平行四边形吗?请说明理由.
【答案】
(1)证明:∵BF=DE,
∴BF﹣EF=DE﹣EF,
∴BE=DF,
在△ABE和△CDF中
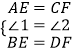
∴△ABE≌△CDF(SAS)
(2)证明:解:四边形四边形ABCD是平行四边形,
理由是:∵△ABE≌△CDF,
∴AB=CD,∠ABE=∠CDF,
∴AB∥CD,
∴四边形ABCD是平行四边形
【解析】(1)求出BE=DF,根据SAS证出两三角形全等即可;(2)根据三角形全等得出AB=CD,∠ABE=∠CDF,推出AB∥CD,根据平行四边形的判定推出即可.
【考点精析】利用平行四边形的判定对题目进行判断即可得到答案,需要熟知两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形.


科目:初中数学 来源: 题型:
【题目】用黑白两种颜色的正六边形地砖按如图所示的方式,拼成若干个图案:

(1)当黑色地砖有1块时,白色地砖有 块,当黑色地砖有2块时,白色地砖有 块;
(2)第n(n为正整数)个图案中,白色地砖有 块;
(3)第几个图案中有2018块白色地砖?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2经过A(﹣2,y1)、B (1,y2)两点,在下列关系式中,正确的是( )
A.y1>0>y2B.y2>0>y1C.y1>y2>0D.y2>y1>0
查看答案和解析>>
科目:初中数学 来源: 题型:
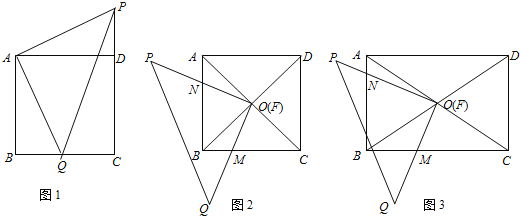
【题目】(1)正方形ABCD与等腰直角三角形PAQ如图1所示重叠在一起,其中∠PAQ=90°,点Q在BC上,连接PD,△ADP与△ABQ全等吗?请说明理由.
(2)如图2,O为正方形ABCD对角线的交点,将一直角三角板FPQ的直角顶点F与点O重合转动三角板使两直角边始终与BC、AB相交于点M、N,使探索OM与ON的数量关系,并说明理由.
(3)如图3,将(2)中的“正方形”改成“长方形”,其它的条件不变,且AB=4,AD=6,FM=x,FN=y,试求y与x之间的函数关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com