
����Ŀ����ͼ����֪��AOB��60�����ڡ�AOB��ƽ����OM����һ��C����DCE��120��������DCE�Ķ������C�غϣ����������߷ֱ���ֱ��OA��OB�ཻ�ڵ�D��E��
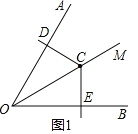
��1������DCE�Ƶ�C��ת��CD��OA��ֱʱ����ͼ1���������OE+OD��OC��������ϵ����˵�����ɣ�
��2���ɣ�ͼ1����λ�ý���DCE�Ƶ�C��ʱ����ת���ǣ�0������90�������߶�OD��OE��OC֮������������������ϵ����д����IJ��룬��˵�����ɣ�
���𰸡���1��OE+OD��![]() OC������������2��OD+OE��
OC������������2��OD+OE��![]() OC��OE��OD��
OC��OE��OD��![]() OC��������
OC��������
��������
��1�����жϳ���OCE��60��������������ǵ����Ǻ����ó�OD��OE��![]() OC�����ɵó����ۣ�
OC�����ɵó����ۣ�
��2�������������ͼ��ͬ��1���ķ�����OF+OG��![]() OC�����жϳ���CFD�ա�CGE���ó�DF��EG���������������ɵó����ۣ�
OC�����жϳ���CFD�ա�CGE���ó�DF��EG���������������ɵó����ۣ�
�⣺��1��OE+OD��![]() OC���������£�
OC���������£�
��OM�ǡ�AOB��ƽ���ߣ�
���AOC����BOC��![]() ��AOB��30����
��AOB��30����
��CD��OA�����ODC��90��
���OCD��60��
���OCE����DCE����OCD��60����
��Rt��OCD��OD��OCcos30����![]() OC��
OC��
ͬ����OE��![]() OC��
OC��
��OD+OE��![]() OC��
OC��
��2��OD+OE��![]() OC��OE��OD��
OC��OE��OD��![]() OC���������£�
OC���������£�
���籸��ͼ1������C��CF��OA�ڵ�F��CG��OB�ڵ�G��
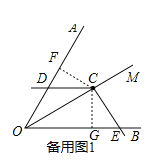
���OFC����OGC��90��
�ߡ�AOB��60����
���FCG��120����
ͬ��1���ķ����ã�OF��![]() OC��OG��
OC��OG��![]() OC��
OC��
��OF+OG��![]() OC��
OC��
��CF��OA��CG��OB���ҵ�C�ڡ�AOB��ƽ�����ϣ�
��CF��CG��
�ߡ�DCE����FCG��120����
���DCF����ECG��
���CFD�ա�CGE��ASA��
��DF��EG��
��OF��OD+DF��span>OD+EG��OG��OE��GE��
��OF+OG��OD+OE��
��OD+OE��![]() OC��
OC��
���籸��ͼ2������C��CF��OA�ڵ�F��CG��OB�ڵ�G��
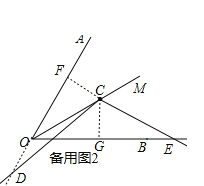
���OFC����OGC��90��
�ߡ�AOB��60����
���FCG��120����
ͬ��1���ķ����ã�OF��![]() OC��OG��
OC��OG��![]() OC��
OC��
��OF+OG��![]() OC��
OC��
��CF��OA��CG��OB���ҵ�C�ڡ�AOB��ƽ�����ϣ�
��CF��CG��
�ߡ�DCE����FCG��120����
���DCF����ECG��
���CFD�ա�CGE��ASA��
��DF��EG��
��OF��DF��OD��EG��OD��OG��OE��GE��
��OF+OG��OE��OD��
��OE��OD��![]() OC��
OC��
�����������߶�OD��OE��OC֮���������ϵΪ��OD+OE��![]() OC��OE��OD��
OC��OE��OD��![]() OC��
OC��


 ��1����Ԫ�¿�������ĩϵ�д�
��1����Ԫ�¿�������ĩϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��Ϊ������ˮƽ����![]() �ϵ�̨�ƣ������ĸ�
�ϵ�̨�ƣ������ĸ�![]() Ϊ
Ϊ![]() .���Ⱦ�Ϊ
.���Ⱦ�Ϊ![]() ������
������![]() ��
��![]() ��
��![]() ʼ����ͬһˮƽ����.
ʼ����ͬһˮƽ����.
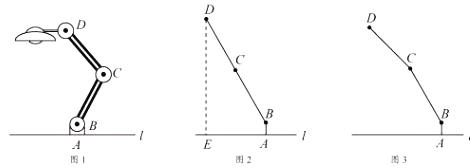
��1����ת����![]() ��
��![]() ��ʹ
��ʹ![]() ��ƽ�ǣ�
��ƽ�ǣ�![]() ����ͼ2�������˶˵�
����ͼ2�������˶˵�![]() ������
������![]() �ĸ߶�
�ĸ߶�![]() .
.
��2������1���е�����![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת��ʹ
��ʱ����ת��ʹ![]() ����ͼ3���ʴ�ʱ���˶˵�
����ͼ3���ʴ�ʱ���˶˵�![]() ������
������![]() �ĸ߶��������˻��Ǽ��٣����ӻ�����˶��٣�����ȷ��
�ĸ߶��������˻��Ǽ��٣����ӻ�����˶��٣�����ȷ��![]() ���ο����ݣ�
���ο����ݣ�![]() ��
��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��E��������ABCD��CD��������һ�㣮
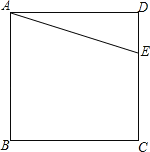
��1���Ե�AΪ���ģ�����ADE˳ʱ����ת90����������ת���ͼ�Σ�
��2����BC���ϻ�һ��F��ʹ��CFE���ܳ�����������ABCD���ܳ���һ�룬���Ҫ˵����ȡ�õ�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺��һ����Բ�������ߵ�һ������ɵķ��ͼ�γ�Ϊ����Բ����
��ͼ��������y��x2��2x��3��x�ύ�ڵ�A��B����y�ύ�ڵ�D����ABΪֱ������x���Ϸ�����Բ��y���ڵ�C����Բ��Բ�ļ�ΪM����ʱ�����Բ������������x���·�������ɵ�ͼ�ξͳ�Ϊ����Բ����
��1��ֱ��д����A��B��C�����꼰����Բ����CD�ij���
A�� ����B�� ����C�� ����CD���� ����
��2�����һ��ֱ���롰��Բ��ֻ��һ�����㣬��ô����ֱ�߽�������Բ�������ߣ�
������C�ġ���Բ�����ߵĽ���ʽ��
������D�ġ���Բ�����ߵĽ���ʽ��
��3���ɣ�2����ù���D�ġ���Բ��������x�ύ���ΪE����F�ǡ���Բ����һ���㣬�����Ƿ����S��CDE��S��CDF���������������F�����ꣻ�������ڣ���˵�����ɣ�
��4����P�ǡ���Բ����һ�㣬�������BPC��60�㣬��BP���ʱ����ֱ��д����P�����꣮
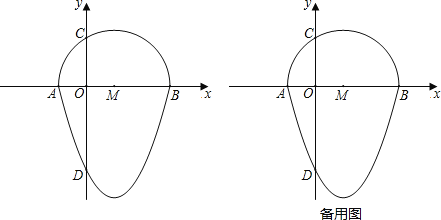
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ����
����![]() Ϊ
Ϊ![]() ���ϵ�һ�����㣨��
���ϵ�һ�����㣨��![]() �����
�����![]() ����
����![]() �غϣ�����
�غϣ�����![]() Ϊ������
������![]() ������
������![]() ��
��![]() ���ڵ�
���ڵ�![]() ������
������![]() ��
��![]() ������
������![]() �ڵ�
�ڵ�![]() .
.
��1����֤��![]() ��
��
��2����![]() ƽ��
ƽ��![]() ʱ����
ʱ����![]() �ij���
�ij���
��3����![]() �ǵ���������ʱ����
�ǵ���������ʱ����![]() �ij���
�ij���
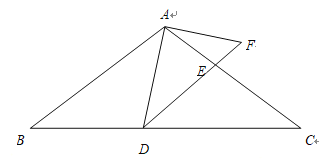
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����������˾�ƻ�����A�ͺ�B�����ֽ���������������A������4����B������7��������310��Ԫ��������A������10����B������15��������700��Ԫ��
��1��A�ͺ�B������ÿ���ļ۸�ֱ��Ƕ�����Ԫ��
��2���ù�˾�ƻ�����A�ͺ�B������������10�������ò�����285��Ԫ����A����������������B���������������������������ʡ�ķ�����������÷���������ã�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����ר���꾭��ij���ͺŵ�����.��֪���ͺ������Ľ���Ϊ![]() ��Ԫ/��������һ��ʱ����֣������ͺ������ۼ۶�Ϊ
��Ԫ/��������һ��ʱ����֣������ͺ������ۼ۶�Ϊ![]() ��Ԫ/��ʱ��ƽ��ÿ���۳�
��Ԫ/��ʱ��ƽ��ÿ���۳�![]() �����ۼ�ÿ����
�����ۼ�ÿ����![]() ��Ԫ��ƽ��ÿ�ܶ��۳�
��Ԫ��ƽ��ÿ�ܶ��۳�![]() ��.
��.
��1�����ۼ�Ϊ![]() ��Ԫ/��ʱ��ƽ��ÿ�ܵ���������Ϊ___________��Ԫ��
��Ԫ/��ʱ��ƽ��ÿ�ܵ���������Ϊ___________��Ԫ��
��2�����õ�ƻ�ƽ��ÿ�ܵ�����������![]() ��Ԫ��Ϊ�˾�����ٿ�棬��ÿ���������ۼۣ�
��Ԫ��Ϊ�˾�����ٿ�棬��ÿ���������ۼۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣�B��C��E��ͬһֱ���ϵ������㣬 �ı���ABCD���ı���CEFG���������Σ�����BG��DE.
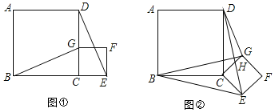
(1)̽��BG��DE֮���������ϵ�� ��֤����Ľ��ۣ�
(2)��������CEFG�Ƶ�C��ƽ����˳ʱ��ת������ͼ����ʾ��λ��ʱ���߶�BG��ED�кι�ϵ? д�����۲�֤��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�У�E��AD���е㣬F��AB����һ�㣬BF=3AF���������ĸ����ۣ�
�١�AEF�ס�DCE��
��CEƽ����DCF��
����B��C��E��F�ĸ�����ͬһ��Բ�ϣ�
��ֱ��EF����DCE�����Բ�����ߣ�
���У���ȷ�ĸ����ǣ� ��

A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com