
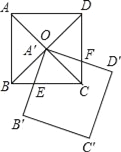
【题目】已知,如图,正方形ABCD的对角线AC,BD相交于点O,正方形A′B′C′D′的顶点A′与点O重合,A′B′交BC于点E,A′D′交CD于点F.
(1)求证:OE=OF;
(2)若正方形ABCD的对角线长为4,求两个正方形重叠部分的面积为__.
【答案】2
【解析】分析:(1)由正方形的性质可以得出△BOE≌△COF,由全等三角形的性质就可以得出OE=OF;
(2)由全等可以得出S△BOE=S△COF,就可以得出S四边形OECF=S△BOC,S△BOC的面积就可以得出结论.
详解:(1)证明:∵正方形ABCD的对角线AC、BD交于点O
∴∠BOC=90°,∠OBC=∠OCD=∠OCF=45°,OB=OC,
∵正方形A'B'C'D'的A'B'交BC于点E,A'D'交CD于点F.
∴∠EOF=90°
∵∠BOE=∠EOF﹣∠EOC=90°﹣∠EOC
∠COF=∠BOC﹣∠EOC=90°﹣∠EOC
∴∠BOE=∠COF.
在△OBE和△OCF中,
∠BOE=∠COF,OB=OC,∠OBC=∠OCF,
∴△BOE≌△COF(ASA).
∴OE=OF;
(2)解:∵△BOE≌△COF,
∴S△BOE=S△COF
∴S△EOC+S△COF=S△EOC+S△BOE,
即S四边形OECF=S△BOC.
∵S△BOC=2,
∴两个正方形重叠部分的面积为2.
故答案为:2.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】为更好宣传“开车不喝酒,喝酒不开车”的驾车理念,某市一家报社设计了如图1的调查问卷(单选),在随机调查了本市10000名司机中的部分司机后,统计整理并制作了如图2所示的统计图: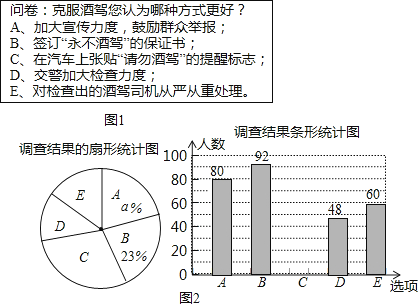
根据以上的信息解答下列问题:
(1)补全条形统计图,并计算扇形统计图中a= .
(2)该市支持选项C的司机大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】去冬今春,我市部分地区遭受了罕见的旱灾,“旱灾无情人有情”.某单位给某乡中小学捐献一批饮用水和蔬菜共320件,其中饮用水比蔬菜多80件.
(1)求饮用水和蔬菜各有多少件?
(2)现计划租用甲、乙两种货车共8辆,一次性将这批饮用水和蔬菜全部运往该乡中小学.已知每辆甲种货车最多可装饮用水40件和蔬菜10件,每辆乙种货车最多可装饮用水和蔬菜各20件.则运输部门安排甲、乙两种货车时有几种方案?请你帮助设计出来;
(3)在(2)的条件下,如果甲种货车每辆需付运费400元,乙种货车每辆需付运费360元.运输部门应选择哪种方案可使运费最少?最少运费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学阅读:
古希腊数学家海伦曾提出一个利用三角形三边之长求面积的公式:若一个三角形的三边长分别为a、b、c,则这个三角形的面积为![]() ,其中
,其中![]() .这个公式称为“海伦公式”.
.这个公式称为“海伦公式”.
数学应用:
如图1,在△ABC中,已知AB=9,AC=8,BC=7.
(1)请运用海伦公式求△ABC的面积;
(2)设AB边上的高为![]() ,AC边上的高
,AC边上的高![]() ,求
,求![]() 的值;
的值;
(3)如图2,AD、BE为△ABC的两条角平分线,它们的交点为I,求△ABI的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形A1B1B2C1 , A2B2B3C2 , A3B3B4C3 , …,AnBnBn+1Cn , 按如图所示放置,使点A1、A2、A3、A4、…、An在射线OA上,点B1、B2、B3、B4、…、Bn在射线OB上.若∠AOB=45°,OB1=1,图中阴影部分三角形的面积由小到大依次记作S1 , S2 , S3 , …,Sn , 则Sn= . 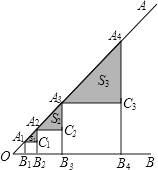
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com