
【题目】在Rt△ABC中,∠C=90°,Rt△ABC绕点A顺时针旋转到Rt△ADE的位置,点E在斜边AB上,连结BD,过点D作DF⊥AC于点F.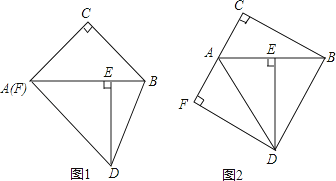
(1)如图1,若点F与点A重合,求证:AC=BC;
(2)若∠DAF=∠DBA,
①如图2,当点F在线段CA的延长线上时,判断线段AF与线段BE的数量关系,并说明理由;
②当点F在线段CA上时,设BE=x,请用含x的代数式表示线段AF.
【答案】
(1)
解:由旋转得,∠BAC=∠BAD,
∵DF⊥AC,
∴∠CAD=90°,
∴∠BAC=∠BAD=45°,
∵∠ACB=90°,
∴∠ABC=45°,
∴AC=CB.
(2)
解:①由旋转得,AD=AB,
∴∠ABD=∠ADB,
∵∠DAF=∠ABD,
∴∠DAF=∠ADB,
∴AF∥BB,
∴∠BAC=∠ABD,
∵∠ABD=∠FAD
由旋转得,∠BAC=∠BAD,
∴∠FAD=∠BAC=∠BAD= ![]() ×180°=60°,
×180°=60°,
由旋转得,AB=AD,
∴△ABD是等边三角形,
∴AD=BD,
在△AFD和△BED中,
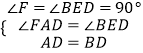 ,
,
∴△AFD≌△BED,
∴AF=BE,
②如图, 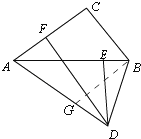
由旋转得,∠BAC=∠BAD,
∵∠ABD=∠FAD=∠BAC+∠BAD=2∠BAD,
由旋转得,AD=AB,
∴∠ABD=∠ADB=2∠BAD,
∵∠BAD+∠ABD+∠ADB=180°,
∴∠BAD+2∠BAD+2∠BAD=180°,
∴∠BAD=36°,
设BD=x,作BG平分∠ABD,
∴∠BAD=∠GBD=36°
∴AG=BG=BC=x,
∴DG=AD﹣AG=AD﹣BG=AD﹣BD,
∵∠BDG=∠ADB,
∴△BDG∽△ADB,
∴ ![]() .
.
∴ ![]() ,
,
∴ ![]() ,
,
∵∠FAD=∠EBD,∠AFD=∠BED,
∴△AFD∽△BED,
∴ ![]() ,
,
∴AF= ![]() x.
x.
【解析】(1)由旋转得到∠BAC=∠BAD,而DF⊥AC,从而得出∠ABC=45°,最后判断出△ABC是等腰直角三角形;
(2)①由旋转得到∠BAC=∠BAD,再根据∠DAF=∠DBA,从而求出∠FAD=∠BAC=∠BAD=60°,最后判定△AFD≌△BED,即可;②根据题意画出图形,先求出角度,得到△ABD是顶角为36°的等腰三角形,再用相似求出, ![]() ,最后判断出△AFD∽△BED,代入即可.此题是几何变换综合题,主要考查了,等腰直角三角形的性质和判定,全等三角形的性质和判定,相似三角形的性质和判定,旋转的性质,解本题的关键是求出顶角为36°的等腰三角形的腰与底的比值,也是本题的难点.
,最后判断出△AFD∽△BED,代入即可.此题是几何变换综合题,主要考查了,等腰直角三角形的性质和判定,全等三角形的性质和判定,相似三角形的性质和判定,旋转的性质,解本题的关键是求出顶角为36°的等腰三角形的腰与底的比值,也是本题的难点.
【考点精析】利用相似三角形的判定与性质对题目进行判断即可得到答案,需要熟知相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
【题目】先阅读下列一段文字,再回答问题:
已知平面内两点P1(x1,y1)、P2(x2,y2),这两点间的距离P1P2=![]() .同时当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间的距离公式可简化为|x2﹣x1|或|y2﹣y1|.
.同时当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间的距离公式可简化为|x2﹣x1|或|y2﹣y1|.
(1)已知点A(2,3)、B(4,2),试求A、B两点间的距离;
(2)已知点A、B在平行于x轴的直线上,点A的横坐标为7,点B的横坐标为5,试求A、B两点间的距离;
(3)已知一个三角形的各顶点坐标为A(﹣2,1)、B(1,4)、C(1﹣a,5),试用含a的式子表示△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形 ABCD 中,AB=6cm,BC=3cm,E 为 CD 的中点.动点 P 从 A 点出发,以每秒1cm 的速度沿 A﹣B﹣C﹣E 运动,最终到达点 E.若点 P 运动时间为 x 秒,则 x=_______时,△APE 的面积等于 6.

查看答案和解析>>
科目:初中数学 来源: 题型:
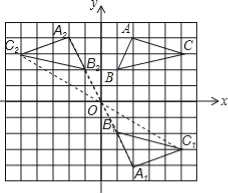
【题目】如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:
(1)画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标.
(2)画出△A1B1C1绕原点O旋转180°后得到的△A2B2C2,并写出点A2的坐标.
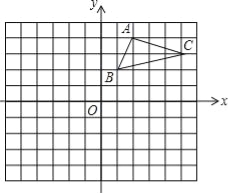
【答案】(1)作图见解析;点A1的坐标(2,﹣4);(2)作图见解析;点A2的坐标(﹣2,4).
【解析】
试题分析:(1)分别找出A、B、C三点关于x轴的对称点,再顺次连接,然后根据图形写出A点坐标;
(2)将△A1B1C1中的各点A1、B1、C1绕原点O旋转180°后,得到相应的对应点A2、B2、C2,连接各对应点即得△A2B2C2.
试题解析:(1)如图所示:点A1的坐标(2,﹣4);
(2)如图所示,点A2的坐标(﹣2,4).
考点:1.作图-旋转变换;2.作图-轴对称变换.
【题型】解答题
【结束】
18
【题目】观察下面的点阵图和相应的等式,探究其中的规律:
(1)认真观察,并在④后面的横线上写出相应的等式.
![]()
①1=1 ②1+2=![]() =3 ③1+2+3=
=3 ③1+2+3=![]() =6 ④ …
=6 ④ …
(2)结合(1)观察下列点阵图,并在⑤后面的横线上写出相应的等式.
![]()
1=12②1+3=22③3+6=32④6+10=42⑤ …
(3)通过猜想,写出(2)中与第n个点阵相对应的等式 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“古诗送郎从军:送郎一路雨飞池,十里江亭折柳枝;离人远影疾行去,归来梦醒度相思.”中,如果用纵轴y表示从军者与送别者行进中离原地的距离,用横轴x表示送别进行的时间,从军者的图象为O→A→B→C,送别者的图象为O→A→B→D,那么下面的图象与上述诗的含义大致吻合的是( )
A. 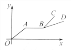 B.
B. 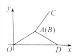 C.
C. 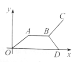 D.
D. 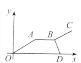
查看答案和解析>>
科目:初中数学 来源: 题型:
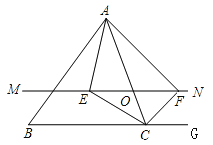
【题目】如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
(3)当点O运动到何处,且△ABC满足什么条件时,四边形AECF是正方形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
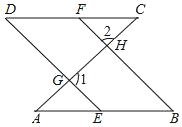
【题目】如图,∠1+∠2=180°,∠B=∠D.说明AB∥CD的理由.
补全下面的说理过程,并在括号内填上适当的理由
解:∵∠1+∠2=180°(已知)
∠2=∠AHB( )
∴ (等量代换)
∴DE∥BF( )
∴∠D=∠ ( )
∵∠ =∠B(等量代换)
∴AB∥CD( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知整数a1,a2,a3,a4,…满足下列条件:a1=0,a2=﹣|a1+1|,a3=﹣|a2+2|,a4=﹣|a3+3|,…,依此类推,则a2018的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,﹣3)
(1)求抛物线的解析式;
(2)点P在抛物线位于第四象限的部分上运动,当四边形ABPC的面积最大时,求点P的坐标和四边形ABPC的最大面积.
(3)直线l经过A、C两点,点Q在抛物线位于y轴左侧的部分上运动,直线m经过点B和点Q,是否存在直线m,使得直线l、m与x轴围成的三角形和直线l、m与y轴围成的三角形相似?若存在,求出直线m的解析式,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com