
【题目】先阅读下列一段文字,再回答问题:
已知平面内两点P1(x1,y1)、P2(x2,y2),这两点间的距离P1P2=![]() .同时当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间的距离公式可简化为|x2﹣x1|或|y2﹣y1|.
.同时当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间的距离公式可简化为|x2﹣x1|或|y2﹣y1|.
(1)已知点A(2,3)、B(4,2),试求A、B两点间的距离;
(2)已知点A、B在平行于x轴的直线上,点A的横坐标为7,点B的横坐标为5,试求A、B两点间的距离;
(3)已知一个三角形的各顶点坐标为A(﹣2,1)、B(1,4)、C(1﹣a,5),试用含a的式子表示△ABC的面积.
【答案】(1)AB=![]() ;(2)AB=2;(3)①当1-a<2,即a>-1时, S△ABC=
;(2)AB=2;(3)①当1-a<2,即a>-1时, S△ABC=![]() a+
a+![]() ,②当1-a>2,即a<-1时,S△ABC=-
,②当1-a>2,即a<-1时,S△ABC=-![]() a-
a-![]() .
.
【解析】
(1)直接利用公式计算即可;
(2)根据两点之间的距离的定义计算即可;
(3)法两种情形分别求解即可解决问题.
(1)AB=![]() =
=![]() .
.
(2)∵已知点A、B在平行于x轴的直线上,点A的横坐标为7,点B的横坐标为5,
∴AB=7-5=2.
(3)由题意,直线AB的解析式为y=x+3,延长AB交直线y=5于N(2,5).
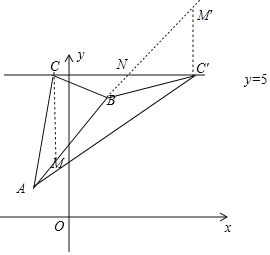
①当1-a<2,即a>-1时,作CM∥y轴交AB于M.则M(1-a,4-a),
∴CM=5-(4-a)=a+1,
∴S△ABC=![]() CM(Bx-Ax)=
CM(Bx-Ax)=![]() (a+1)3=
(a+1)3=![]() a+
a+![]() .
.
②当1-a>2,即a<-1时,同法可得S△ABC=-![]() a-
a-![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
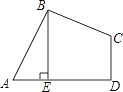
【题目】如图,在四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,且四边形ABCD的面积为4,则BE等于________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上两点A、B对应的数分别为﹣1、3,点P为数轴上一动点,其对应的数为x.
(1)若点P到点A,点B的距离相等,点P对应的数是 .
(2)数轴上,点P到点A、点B的距离之和为5,则x的值为 ;
(3)当点P以每秒1个单位长度的速度从原点O向左运动,同时点B以每秒3个单位长度的速度沿数轴向左运动(点A保持不动),当点P到点A、点B的距离相等时,求运动时间t的值?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果,绘制出了如下尚不完整的统计图表。
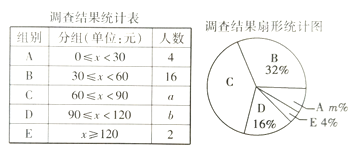
请根据以上图表,解答下列问题:
(1)这次被调查的同学共有_____________人,a+b=______________,m=________;
(2)求扇形统计图中扇形C的圆心角度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①表示的是某商场2012年前四个月中两个月的商品销售额的情况,图②表示的是商场家电部各月销售额占商场当月销售总额的百分比情况,观察图①、图②解答下列问题:
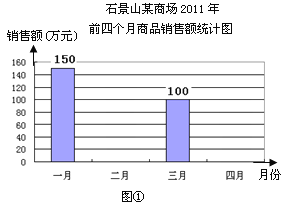
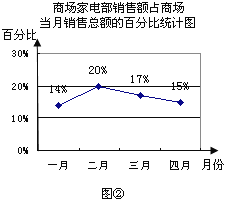
(1)商场前四个月财务结算显示四月份商场的商品销售额比一月份下降了20%,请你求出商场四月份的销售额;
(2)若商场前四个月的商品销售总额一共是500万元,请你根据这一信息将图①中的统计图补充完整;
(3)小明观察图②后认为,商场家电部四月份的销售额比三月份减少了,你同意他的看法吗?请你说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆货车从超市出发,向东走了1千米,到达小明家,继续向东走了3千米到达小兵家,然后西走了10千米,到达小华家,最后又向东走了6千米结束行程.
(1)如果以超市为原点,以向东为正方向,用1个单位长度表示1千米,请你在下面的数轴上表示出小明家、小兵家和小华家的具体位置.

(2)请你通过计算说明货车最后回到什么地方?
(3)如果货车行驶1千米的用油量为0.25升,请你计算货车从出发到结束行程共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李和小陆从A地出发,骑自行车沿同一条路行驶到B地,他们离出发地的距离S(单位:km)和行驶时间t(单位:h)之间的函数关系的图象如图所示,根据图中的信息,有下列说法:
(1)他们都行驶了20 km;
(2)小陆全程共用了1.5h;
(3)小李和小陆相遇后,小李的速度小于小陆的速度
(4)小李在途中停留了0.5h。
其中正确的有
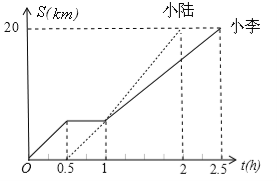
A.4个 B.3个 C.2个 D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°,Rt△ABC绕点A顺时针旋转到Rt△ADE的位置,点E在斜边AB上,连结BD,过点D作DF⊥AC于点F.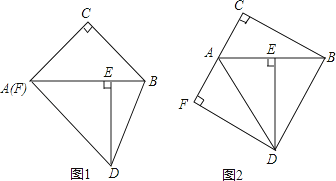
(1)如图1,若点F与点A重合,求证:AC=BC;
(2)若∠DAF=∠DBA,
①如图2,当点F在线段CA的延长线上时,判断线段AF与线段BE的数量关系,并说明理由;
②当点F在线段CA上时,设BE=x,请用含x的代数式表示线段AF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com