
分析 (1)根据负整数指数幂、零指数幂、绝对值、平方进行计算即可;
(2)根据同底数幂的乘法、积的乘方和幂的乘方进行计算即可;
(3)根据多项式乘以多项式、单项式乘以多项式进行计算即可;
(4)根据完全平方公式和平方差公式进行计算即可.
解答 解:(1)-22+(-$\frac{1}{2}$)-2-(π-5)0-|-3|
=-4+4-1-3
=-4;
(2)(-2x)2•(x2)3•(-x)2
=4x2•x6•x2
=4x10;
(3)原式=x2+x-2-3x2-9x
=-2x2-8x-2;
(4)原式=x2-2xy+y2-x2+4y2
=-2xy+5y2.
点评 本题考查了整式的混合运算,零指数幂、负整数指数幂,熟记公式和运算性质是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在⊙O中,AB是弦,过点A的切线交BO的延长线于点C,若⊙O的半径为3,∠C=20°,则$\widehat{AB}$的长为$\frac{11}{6}π$.
如图,在⊙O中,AB是弦,过点A的切线交BO的延长线于点C,若⊙O的半径为3,∠C=20°,则$\widehat{AB}$的长为$\frac{11}{6}π$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
| 摸到白球的次数m | 63 | 124 | 178 | 302 | 481 | 599 | 1803 |
| 摸到白球的频率$\frac{m}{n}$ | 0.63 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,排球在黑白两色的方砖上随机滚动,落在每块方砖上的可能性相同(若落在线上,则随机滚动一次).
如图,排球在黑白两色的方砖上随机滚动,落在每块方砖上的可能性相同(若落在线上,则随机滚动一次).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
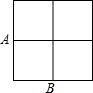 如图,在2×2的正方形网格中四个小正方形的顶点叫格点,已经取定格点A和B,在余下的格点中任取一点C,使△ABC为直角三角形的概率是$\frac{4}{7}$.
如图,在2×2的正方形网格中四个小正方形的顶点叫格点,已经取定格点A和B,在余下的格点中任取一点C,使△ABC为直角三角形的概率是$\frac{4}{7}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com