
����Ŀ����ʦ���ݳ�������֦��ij�س��ۣ���������ǰ��������50������ʻ����Сʱ��ͼ���ڼ���վ������������������ʣ������y����������ʻʱ��t��Сʱ��֮��Ĺ�ϵ��ͼ��ʾ�� 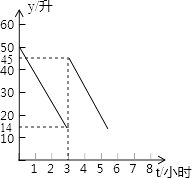
��1��������ʻСʱ����ͣ���;��������
��2�������ǰ����ʣ������y����ʻʱ��t�ĺ�����ϵʽ��
��3����֪����ǰ������������70ǧ��/Сʱ������ʻ���������վ��Ŀ�ĵ�210ǧ�ף�Ҫ����Ŀ�ĵأ��������е����Ƿ��ã���˵�����ɣ�
���𰸡�
��1��3��31
��2���⣺��y��t�ĺ�����ϵʽ��y=kt+b��k��0�����������⣬����0��50����3��14������
�ã� ![]()
��ˣ�����ǰ����ʣ����y����ʻʱ��t�ĺ�����ϵʽ�ǣ�y=��12t+50��
��3���⣺��ͼ��֪����ÿСʱ���ͣ�50��14����3=12��������
��������Ҫ����210��70��12=36����������Ϊ45����36�������������е����ã�
����������1��������ͼ�ɿ��������͵�ʱ��ͼ���������2���躯��ϵʽy=kx+b������0��50����3��14�����뼴����⣻��3����·�̺��ٶ����ʱ�䣬�����ÿСʱ�����������ж����Ƿ��ã�


 ���⿼����Ԫ���Ծ�ϵ�д�
���⿼����Ԫ���Ծ�ϵ�д� ��У���˳�̾�ϵ�д�
��У���˳�̾�ϵ�д� ��У���һ��ͨϵ�д�
��У���һ��ͨϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������Ŀڴ���װ��4���ֱ������1��2��3��4��С�����ǵ���״����С��ȫ��ͬ��С���ȴӿڴ����������һ��С�������Ϊx��Сӱ��ʣ�µ�3�������������һ��С�������Ϊy������ȷ���˵�P�����꣨x��y����
��1��С������������3��С��ĸ����� ��
��2���������б�������״ͼ�����P��x��y���ں���y=��x+5ͼ���ϵĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ı���ABCD�������Σ�E��F�ֱ���DC��CB���ӳ����ϵĵ㣬��DE=BF������AE��AF��EF�� 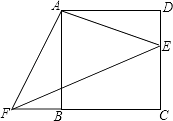
��1����֤����ADE�ա�ABF��
��2����BC=8��DE=6�����AEF�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ԡ�ABC�ı�AB��ACΪ�߷ֱ�����������ֱ�ǡ�ABD�͵���ֱ�ǡ�ACE������CD��BE��DE 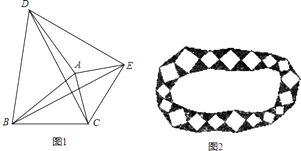
��1��֤������ADC�ա�ABE��
��2�����жϡ�ABC���ADE���֮��Ĺ�ϵ����˵�����ɣ�
��3����С·������ͨ�ģ���ͼ2��ʾ��С·�ɰ�ɫ�������δ���ʯ�ͺ�ɫ�������δ���ʯ�̳ɣ���֪�м�����������ε����֮����aƽ���ף���Ȧ�����������ε����֮����bƽ���ף�����С·һ��ռ��ƽ���ף�������д���̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=AC=10����D�DZ�BC��һ���㣨����B��C�غϣ�����ADE=��B=����DE��AC�ڵ�E����cos��= ![]() �����н��ۣ��١�ADE�ס�ACD���ڵ�BD=6ʱ����ABD���DCEȫ�ȣ��ۡ�DCEΪֱ��������ʱ��BDΪ8����0��CE��6.4��������ȷ�Ľ����� �� ��������Ϊ��ȷ���۵���Ŷ����ϣ�
�����н��ۣ��١�ADE�ס�ACD���ڵ�BD=6ʱ����ABD���DCEȫ�ȣ��ۡ�DCEΪֱ��������ʱ��BDΪ8����0��CE��6.4��������ȷ�Ľ����� �� ��������Ϊ��ȷ���۵���Ŷ����ϣ� 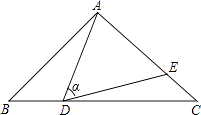
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=90�㣬AC=3��BC=4����F�ڱ�AC�ϣ�����CF=1����EΪ��BC�ϵĶ��㣬����CEF��ֱ��EF���ۣ���C���ڵ�P�������P����AB�������Сֵ�� �� 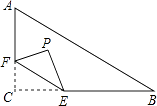
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˼����С����̽������ֱ�ߵ�λ�ù�ϵ��������ʱ�������ˡ��д������Ρ��������������ഹֱ�������γ�Ϊ���д������Ρ�����ͼ��1����ͼ��2����ͼ��3���У�AM��BN�ǡ�ABC�����ߣ�AM��BN�ڵ�P�����ABC�����������ξ�Ϊ���д������Ρ�����BC=a��AC=b��AB=c��
��1��������̽����
��ͼ1����tan��PAB=1��c=4 ![]() ʱ��a= �� b=��
ʱ��a= �� b=��
��ͼ2������PAB=30�㣬c=2ʱ��a= �� b=��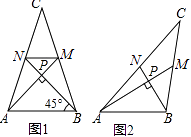
��2��������֤����
����۲죨1���еļ�����������a2��b2��c2����֮��Ĺ�ϵ���õ�ʽ��ʾ������������ͼ3֤����Ľ��ۣ�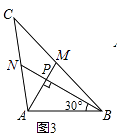
��3������չ֤����
��ͼ4��ABCD�У�E��F�ֱ���AD��BC�����ȷֵ㣬��AD=3AE��BC=3BF������AF��BE��CE����BE��CE��E��AF��BE�ཻ��G��AD=3 ![]() ��AB=3����AF�ij���
��AB=3����AF�ij���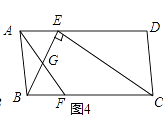
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���μ�ij�����������Ŀ��������������ѡ���˳��ͨ�أ���һ����ѡ����3��ѡ��ڶ�����ѡ����4��ѡ���������С�������ᣬ����С������һ����������û���ã�ʹ�á�������������������ȥ������һ���һ������ѡ���
��1�����С����һ�ⲻʹ�á�����������ôС����Ե�һ����ĸ����� ��
��2�����С���������������ڵڶ���ʹ�ã�������״ͼ�����б�������С��˳��ͨ�صĸ��ʣ�
��3���Ӹ��ʵĽǶȷ������㽨��С���ڵڼ���ʹ�á�����������ֱ��д���𰸣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ�����н��ۣ���b��0����c��0����a+c��b����b2��4ac��0��������ȷ�ĸ����ǣ������� 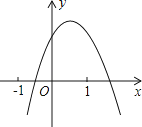
A.1
B.2
C.3
D.4
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com