练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
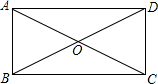
    13．如图，在矩形ABCD中，对角线AC、BD相交于点O，∠AOB=60°，AB=5，则AD的长是5$\sqrt{3}$．

    分析 根据矩形性质得出AC=2AO，BD=2BO，AC=BD，推出AO=OB，得出等边三角形AOB，求出AO，即可得出答案．

    解答 解：∵四边形ABCD是矩形，
    ∴AC=2AO，BD=2BO，AC=BD，
    ∴AO=OB，
    ∵∠AOB=60°，
    ∴△AOB是等边三角形，
    ∴∠ABO=60°，
    ∴AD=AB•tan60°=5$\sqrt{3}$．
    故答案为：5$\sqrt{3}$．

    点评 本题考查了等边三角形的性质和判定，矩形的性质的应用，注意：矩形的对角线互相平分且相等．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017届江苏省盐都市九年级下学期第一次学情调研数学试卷（解析版） 题型：填空题

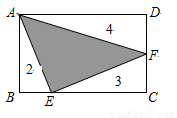
    如图，矩形ABCD被分成四部分，其中△ABE、△ECF、△ADF的面积分别为2、3、4，

    则△AEF的面积为______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．在平面直角坐标系xOy中，抛物线C1：y=mx2-2mx+m+4与y轴交于点A（0，3），与x轴交于点B、C（点B在点C左侧）．
    （1）求该抛物线的解析式；
    （2）求点B的坐标；
    （3）若抛物线C2：y=a（x-1）2-1（a≠0）与线段AB恰有一个公共点，结合函数的图象，求a的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．设二次函数y1=a（x-m）（x-n）（a≠0，m≠n）的图象与一次函数y2=dx+e（d≠0）的图象交于点（m，0），若函数y=y2+y1的图象与x轴仅有一个交点，则（　　）
    A．a（m-n）=dB．a（n-m）=dC．a（m-n）2=dD．a（m+n）2=d

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．一个多边形除去一个内角之外，其余内角之和为2670°，求这个多边形的边数和少加的内角的大小．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

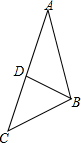    18．如图，在△ABC中，D是边AC上一点，连接BD，给出下列条件：①∠ABD=∠ACB；②AB2=AD•AC；③∠A=∠ABD；④AB•BC=AC•BD．其中单独能够判定△ABD∽△ACB的个数是（　　）
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．下列说法中，不正确的是（　　）
    A．所有的负分数都是有理数B．所有的正整数都是有理数
    C．$\frac{5}{2}$是有理数D．0不是有理数

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．二次函数y=ax2+bx+c（a，b，c为常数，a＜0）的图象经过点（-1，1），（4，-4）．下列结论：
    ①$\frac{a}{c}$＜0；
    ②当x＞1时，y的值随x值的增大而减小；
    ③x=4是方程ax2+（b+1）x+c=0的一个根；
    ④当-1＜x＜4时，ax2+（b+1）x+c＞0．
    其中正确的是（　　）
    A．①③B．①②④C．①③④D．②③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．如图，在△ABC中，AB=AC=5cm，BC=6cm，AD⊥BC于D．动点E从点C出发，以1cm/s的速度沿C→A的方向运动．作EF∥AB，交BC于点F，连接DE．同时动点P由点A出发，沿A→B的方向以相同的速度运动．设运动时间为ts（0＜t＜5）．
    （1）当t为何值时，四边形PBFE是平行四边形？
    （2）当t为何值时，△DEF的面积为$\frac{3}{4}$cm2？请写出求解过程；
    （3）是否存在某一时刻t，使得△PEF是等腰三角形？若存在，直接写出此时t的值；若不存在，请说明理由．

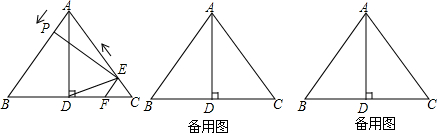
    查看答案和解析>>

    同步练习册答案