
【题目】某区在实施居民用水管理前,随机调查了部分家庭(单位:户)去年的月均用水量(单位:t),并将调查数据进行整理,绘制出如下不完整的统计图表:

请解答以下问题:
(1)把上面的频数分布表和频数分布直方图补充完整;
(2)若该小区有2000户家庭,根据此次随机抽查的数据估计,该小区月均用水量不低于20t的家庭有多少户?
(3)为了鼓励节约用水,要确定一个月均用水量的标准,超出该标准的部分按1.5倍价格收费,若要使68%的家庭水费支出不受影响,那么,你觉得家庭月均用水量应定为多少?
【答案】(1)见解析;(2)240户;(3)15t.
【解析】
(1)根据月用水量在0≤x<5范围的频数与百分比可得调查的总户数,从而可求得用水量在10≤x<15的频数以及20≤x<25的频率,据此补全图、表即可;
(2)用2000乘以月少水量不低于20t的家庭所占的比例即可;
(3)根据各分组的百分比进行判断即可得.
(1)∵被调查的总数量为6÷12%=50(户),
∴10≤x<15的频数为50×32%=16(户)、20≤x<25的频率为4÷50=0.08=8%,
补全图形如下:
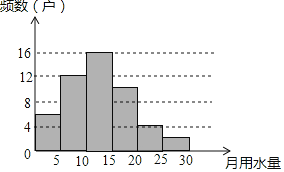
月均用水量 | 频数 | 百分比 |
0≤x<5 | 6 | 12% |
5≤x<10 | 12 | 24% |
10≤x<15 | 16 | 32% |
15≤x<20 | 10 | 20% |
20≤x<25 | 4 | 8% |
25≤x<30 | 2 | 4% |
合计 | 50 | 100% |
(2)估计该小区月均用水量不低于20t的家庭有2000×(8%+4%)=240户;
(3)∵前三个分组的频率之和为12%+24%+32%=68%,
∴家庭月均用水量应定为15t.


科目:初中数学 来源: 题型:
【题目】如图,已知AB是O的直径,点C在O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.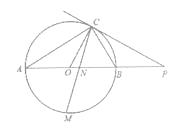
(1)求证:PC是O的切线;
(2)求证:BC= ![]() AB;
AB;
(3)点M是弧AB的中点,CM交AB于点N,若AB=4,求MN·MC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(0,1)、点B(0,1+t)、C(0,1﹣t)(t>0),点P在以D(3,3)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则t的最小值是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点E在AC的延长线上,有下列条件∠1=∠2,②∠3=∠4,③∠A=∠DCE,④∠D=∠DCE,⑤∠A+∠ABD=180°,⑥∠A+∠ACD=180°,其中能判断AB∥CD的是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学体育组因教学需要本学期购进篮球和排球共100个,共花费2600元,已知篮球的单价是20元![]() 个,排球的单价是30元
个,排球的单价是30元![]() 个.
个.
![]() 篮球和排球各购进了多少个
篮球和排球各购进了多少个![]() 列方程组解答
列方程组解答![]() ?
?
![]() 因该中学秋季开学成立小学部,教学资源实现共享,体育组提出还需购进同样的篮球和排球共30个,但学校要求花费不能超过800元,那么排球最多能购进多少个
因该中学秋季开学成立小学部,教学资源实现共享,体育组提出还需购进同样的篮球和排球共30个,但学校要求花费不能超过800元,那么排球最多能购进多少个![]() 列不等式解答
列不等式解答![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一条笔直的公路l穿过草原,公路边有一消防站A,距离公路5 ![]() 千米的地方有一居民点B,A、B的直线距离是10
千米的地方有一居民点B,A、B的直线距离是10 ![]() 千米.一天,居民点B着火,消防员受命欲前往救火.若消防车在公路上的最快速度是80千米/小时,而在草地上的最快速度是40千米/小时,则消防车在出发后最快经过小时可到达居民点B.(友情提醒:消防车可从公路的任意位置进入草地行驶.)
千米.一天,居民点B着火,消防员受命欲前往救火.若消防车在公路上的最快速度是80千米/小时,而在草地上的最快速度是40千米/小时,则消防车在出发后最快经过小时可到达居民点B.(友情提醒:消防车可从公路的任意位置进入草地行驶.) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,点P从点C开始沿射线CA方向以1cm/s的速度运动;同时,点Q也从点C开始沿射线CB方向以3cm/s的速度运动.
(1)几秒后△PCQ的面积为3cm2?此时PQ的长是多少?(结果用最简二次根式表示)
(2)几秒后以A、B、P、Q为顶点的四边形的面积为22cm2?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,∠A=60°,点E,F分别在AB,AC上,把∠A沿着EF对折,使点A落在BC上点D处,且使ED⊥BC. 
(1)猜测AE与BE的数量关系,并说明理由;
(2)求证:四边形AEDF是菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com