
【题目】已知:如图,在长方形![]() 中,AB=4cm,BC=6cm,点
中,AB=4cm,BC=6cm,点![]() 为
为![]() 中点,如果点
中点,如果点![]() 在线段
在线段![]() 上以每秒2cm的速度由点
上以每秒2cm的速度由点![]() 向点
向点![]() 运动,同时,点
运动,同时,点![]() 在线段
在线段![]() 上由点
上由点![]() 向点
向点![]() 运动.设点
运动.设点![]() 运动时间为
运动时间为![]() 秒,若某一时刻△BPE与△CQP全等,求此时
秒,若某一时刻△BPE与△CQP全等,求此时![]() 的值及点
的值及点![]() 的运动速度.
的运动速度.

【答案】见解析
【解析】
由∠B=∠C=90°,可知存在以下两种情况使△BPE≌△CQP,(1)当BP=CP,BE=CQ时;(2)当BP=CQ,BE=CP时;设点Q的运动的时间为vcm/s,则由已知易得BP=2t,CP=6-2t,BE=2,CQ=vt,由此根据上述两种情况分别列出关于t和v的方程,解方程即可求得对应的t和v的值.
设点 ![]() 的运动速度为v cm/s,则
的运动速度为v cm/s,则 ![]() ,
,![]() ,
,![]() ,
,![]() .
.
∵∠B=∠C=90°,
∴存在以下两种情况使△BPE≌△CPQ.
(1)当BP=CP,BE=CQ时,△BPE≌△CPQ,此时有:
![]() ,
,![]() ,
,
解得:![]() ,
,![]() ;
;
(2)当当BP=CQ,BE=CP时,△BPE≌△CPQ,
此时有:![]() ,
,![]() .
.
解得:![]() ,
,![]() .
.
综上所述,![]() 的值为
的值为 ![]() 秒,
秒,![]() 点的速度为
点的速度为![]() ;或
;或![]() 的值为
的值为![]() 秒,
秒,![]() 点的速度为2 cm/s.
点的速度为2 cm/s.


科目:初中数学 来源: 题型:
【题目】模型与应用.
(模型)
(1)如图①,已知AB∥CD,求证∠1+∠MEN+∠2=360°.

(应用)
(2)如图②,已知AB∥CD,则∠1+∠2+∠3+∠4+∠5+∠6的度数为 .

如图③,已知AB∥CD,则∠1+∠2+∠3+∠4+∠5+∠6+…+∠n的度数为 .

(3)如图④,已知AB∥CD,∠AM1M2的角平分线M1 O与∠CMnMn-1的角平分线MnO交于点O,若∠M1OMn=m°.

在(2)的基础上,求∠2+∠3+∠4+∠5+∠6+……+∠n-1的度数.(用含m、n的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与x轴交于点A,与反比例函数y= ![]() (x>0)的图象交于点B(2,n),过点B作BC⊥x轴于点C,点P(3n﹣4,1)是该反比例函数图象上的一点,且∠PBC=∠ABC,求反比例函数和一次函数的表达式.
(x>0)的图象交于点B(2,n),过点B作BC⊥x轴于点C,点P(3n﹣4,1)是该反比例函数图象上的一点,且∠PBC=∠ABC,求反比例函数和一次函数的表达式. 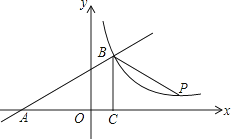
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是由几个相同的边长为1的小立方块搭成的几何体.
(1)请画出这个几何体的三视图;
(2)根据三视图,这个几何体的表面积为 个平方单位(包括底面积);
(3)若上述小立方块搭成的几何体的俯视图不变,各位置的小立方块个数可以改变(总数目不变),则搭成的几何体的表面积最大为 个平方单位(包括底面积) .


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=k1x+b与x轴,y轴相交于P,Q两点,则y= ![]() 的图象相交于A(﹣2,m),B(1,n)两点,连接OA,OB,给出下列结论:①k1k2<0;②m+
的图象相交于A(﹣2,m),B(1,n)两点,连接OA,OB,给出下列结论:①k1k2<0;②m+ ![]() n=0;③S△AOP=S△BOQ;④不等式k1x+b>
n=0;③S△AOP=S△BOQ;④不等式k1x+b> ![]() 的解集在x<﹣2或0<x<1,其中正确的结论是( )
的解集在x<﹣2或0<x<1,其中正确的结论是( ) 
A.②③④
B.①②③④
C.③④
D.②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,按如下步骤作图: ①分别以A,C为圆心,大于 ![]() AC的长为半径画弧,两弧交于P,Q两点;
AC的长为半径画弧,两弧交于P,Q两点;
②作直线PQ,分别交AB,AC于点E,D,连接CE;
③过C作CF∥AB交PQ于点F,连接AF.
(1)求证:△AED≌△CFD;
(2)求证:四边形AECF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.
小明的思路是:如图2,过P作PE∥AB,通过平行线性质,可得∠APC=50°+60°=110°.
问题迁移:
(1)如图3,AD∥BC,点P在射线OM上运动,当点P在A、B两点之间运动时,∠ADP=∠α,∠BCP=∠β.∠CPD、∠α、∠β之间有何数量关系?请说明理由;
(2)在(1)的条件下,如果点P在A、M两点之间和B、O两点之间上运动时(点P与点A、B、O三点不重合),请你分别直接写出∠CPD、∠α、∠β之间的数量关系.
 ,图1)
,图1)  ,图2)
,图2)
 ,图3)
,图3)  ,备用图)
,备用图)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线AB,CD相交于点O,OE平分∠AOD,FO⊥AB,垂足为O,![]() ∠BOD=∠DOE.
∠BOD=∠DOE.
(1)求∠BOF的度数;
(2)请写出图中与∠BOD相等的所有的角.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com