
ЁОЬтФПЁПФЃаЭгыгІгУ.
ЃЈФЃаЭЃЉ
ЃЈ1ЃЉШчЭМЂйЃЌвбжЊABЁЮCDЃЌЧѓжЄЁЯ1ЃЋЁЯMENЃЋЁЯ2ЃН360Ёу.

ЃЈгІгУЃЉ
ЃЈ2ЃЉШчЭМЂкЃЌвбжЊABЁЮCDЃЌдђЁЯ1+ЁЯ2+ЁЯ3+ЁЯ4+ЁЯ5+ЁЯ6ЕФЖШЪ§ЮЊ ЃЎ

ШчЭМЂлЃЌвбжЊABЁЮCDЃЌдђЁЯ1+ЁЯ2+ЁЯ3+ЁЯ4+ЁЯ5+ЁЯ6ЃЋЁЃЋЁЯnЕФЖШЪ§ЮЊ ЃЎ

ЃЈ3ЃЉШчЭМЂмЃЌвбжЊABЁЮCDЃЌЁЯAM1M2ЕФНЧЦНЗжЯпM1 OгыЁЯCMnMnЃ1ЕФНЧЦНЗжЯпMnOНЛгкЕуOЃЌШєЁЯM1OMnЃНmЁуЃЎ

дкЃЈ2ЃЉЕФЛљДЁЩЯЃЌЧѓЁЯ2+ЁЯ3+ЁЯ4+ЁЯ5+ЁЯ6ЃЋЁЁЃЋЁЯnЃ1ЕФЖШЪ§ЃЎЃЈгУКЌmЁЂnЕФДњЪ§ЪНБэЪОЃЉ
ЁОД№АИЁПЃЈ1ЃЉжЄУїМћНтЮіЃЛЃЈ2ЃЉ900Ёу ЃЌ180Ёу(nЃ1)ЃЛЃЈ3ЃЉ(180nЃ180Ѓ2m)Ёу
ЁОНтЮіЁПЃЈ1ЃЉЙ§ЕуEзїEFЁЮCDЃЌИљОнЦНаагкЭЌвЛжБЯпЕФСНЬѕжБЯпЛЅЯрЦНааПЩЕУEFЁЮABЃЌИљОнСНжБЯпЦНааЃЌЭЌХдФкНЧЛЅВЙПЩЕУЁЯ1ЃЋЁЯMEFЃН180ЁуЃЌЁЯ2ЃЋЁЯNEFЃН180ЁуЃЌМДПЩЕУЁЯ1ЃЋЁЯ2ЃЋЁЯMENЃН360Ёу ЃЛЃЈ2ЃЉЂйЗжБ№Й§EЕуЃЌFЕуЃЌGЕуЃЌHЕузїL1ЃЌL2ЃЌL3ЃЌL4ЦНаагкABЃЌРћгУЃЈ1ЃЉЕФЗНЗЈПЩЕУЁЯ1+ЁЯ2+ЁЯ3+ЁЯ4+ЁЯ5+ЁЯ6=180ЁС5=900ЁуЃЛЂкгЩЩЯУцЕФНтЬтЗНЗЈПЩЕУД№АИЃЛЃЈ3ЃЉЙ§ЕуOзїSRЁЮABЃЌИљОнЦНаагкЭЌвЛжБЯпЕФСНЬѕжБЯпЛЅЯрЦНааПЩЕУSRЁЮCDЃЌИљОнСНжБЯпЦНааЃЌФкДэНЧЯрЕШПЩЕУЁЯAM1OЃНЁЯM1ORЃЌЁЯC MnOЃНЁЯMnORЃЌЫљвдЁЯA M1OЃЋЁЯCMnOЃНЁЯM1ORЃЋЁЯMnORЃЌМДПЩЕУЁЯA M1OЃЋЁЯCMnOЃНЁЯM1OMnЃНmЁуЃЌИљОнНЧЦНЗжЯпЕФЖЈвхПЩЕУЁЯAM1M2ЃН2ЁЯA M1OЃЌЁЯCMnMn-1ЃН2ЁЯCMnOЃЌгЩДЫПЩЕУЁЯAM1M2ЃЋЁЯCMnMn-1ЃН2ЁЯAM1OЃЋ2ЁЯCMnOЃН2ЁЯM1OMnЃН2mЁуЃЌгжвђЁЯA M1EЃЋЁЯ2+ЁЯ3+ЁЯ4+ЁЯ5+ЁЯ6ЃЋЁЁЃЋЁЯnЃ1ЃЋЁЯCMnMn-1ЃН180Ёу(nЃ1)ЃЌгЩДЫПЩЕУ
ЁЯ2+ЁЯ3+ЁЯ4+ЁЯ5+ЁЯ6ЃЋЁЃЋЁЯnЃ1ЃН(180nЃ180Ѓ2m)Ёу.
ЁОФЃаЭЁП
ЃЈ1ЃЉШчЭМЂйЃЌвбжЊABЁЮCDЃЌЧѓжЄЁЯ1ЃЋЁЯ2ЃЋЁЯMENЃН360Ёу.
жЄУїЃКЙ§ЕуEзїEFЁЮCDЃЌ
ЁпABЁЮCDЃЌ
ЁрEFЁЮABЃЌ
ЁрЁЯ1ЃЋЁЯMEFЃН180ЁуЃЌ
ЭЌРэЁЯ2ЃЋЁЯNEFЃН180Ёу
ЁрЁЯ1ЃЋЁЯ2ЃЋЁЯMENЃН360Ёу
ЁОгІгУЁП
ЃЈ2ЃЉ900Ёу ЃЌ 180Ёу(nЃ1)
ЗжБ№Й§EЕуЃЌFЕуЃЌGЕуЃЌHЕузїL1ЃЌL2ЃЌL3ЃЌL4ЦНаагкABЃЌРћгУЃЈ1ЃЉЕФЗНЗЈПЩЕУЁЯ1+ЁЯ2+ЁЯ3+ЁЯ4+ЁЯ5+ЁЯ6=180ЁС5=900ЁуЃЛ

гЩЩЯУцЕФНтЬтЗНЗЈПЩЕУЃКЁЯ1+ЁЯ2+ЁЯ3+ЁЯ4+ЁЯ5+ЁЯ6ЃЋЁЃЋЁЯn=180Ёу(nЃ1)ЃЛ
ЃЈ3ЃЉЙ§ЕуOзїSRЁЮABЃЌ

ЁпABЁЮCDЃЌ
ЁрSRЁЮCDЃЌ
ЁрЁЯAM1OЃНЁЯM1OR
ЭЌРэЁЯC MnOЃНЁЯMnOR
ЁрЁЯA M1OЃЋЁЯCMnOЃНЁЯM1ORЃЋЁЯMnORЃЌ
ЁрЁЯA M1OЃЋЁЯCMnOЃНЁЯM1OMnЃНmЁуЃЌ
ЁпM1OЦНЗжЁЯAM1M2ЃЌ
ЁрЁЯAM1M2ЃН2ЁЯA M1OЃЌ
ЭЌРэЁЯCMnMn-1ЃН2ЁЯCMnOЃЌ
ЁрЁЯAM1M2ЃЋЁЯCMnMn-1ЃН2ЁЯAM1OЃЋ2ЁЯCMnOЃН2ЁЯM1OMnЃН2mЁуЃЌ
гжЁпЁЯA M1EЃЋЁЯ2+ЁЯ3+ЁЯ4+ЁЯ5+ЁЯ6ЃЋЁЁЃЋЁЯnЃ1ЃЋЁЯCMnMn-1ЃН180Ёу(nЃ1)ЃЌ
ЁрЁЯ2+ЁЯ3+ЁЯ4+ЁЯ5+ЁЯ6ЃЋЁЃЋЁЯnЃ1ЃН(180nЃ180Ѓ2m)Ёу


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЙЄГЇМЦЛЎЩњВњAЁЂBСНжжВњЦЗЙВ50МўЃЌашЙКТђМзЁЂввСНжжВФСЯЃЎЩњВњвЛМўAВњЦЗашМзжжВФСЯ30ЧЇПЫЁЂввжжВФСЯ10ЧЇПЫЃЛЩњВњвЛМўBВњЦЗашМзЁЂввСНжжВФСЯИї20ЧЇПЫЃЎОВтЫуЃЌЙКТђМзЁЂввСНжжВФСЯИї1ЧЇПЫЙВашзЪН№40дЊЃЌЙКТђМзжжВФСЯ2ЧЇПЫКЭввжжВФСЯ3ЧЇПЫЙВашзЪН№105дЊЃЎ
ЃЈ1ЃЉМзЁЂввСНжжВФСЯУПЧЇПЫЗжБ№ЪЧЖрЩйдЊЃП
ЃЈ2ЃЉЯжЙЄГЇгУгкЙКТђМзЁЂввСНжжВФСЯЕФзЪН№ВЛГЌЙ§38000дЊЃЌЧвЩњВњBВњЦЗВЛЩйгк28МўЃЌЮЪЗћКЯЬѕМўЕФЩњВњЗНАИгаФФМИжжЃП
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌШєЩњВњвЛМўAВњЦЗашМгЙЄЗб200дЊЃЌЩњВњвЛМўBВњЦЗашМгЙЄЗб300дЊЃЌгІбЁдёФФжжЩњВњЗНАИЃЌЪЙЩњВњет50МўВњЦЗЕФГЩБОзюЕЭЃПЃЈГЩБО=ВФСЯЗб+МгЙЄЗбЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЦНааЫФБпаЮABCDЕФЖЅЕуAдкЕкШ§ЯѓЯоЃЌЖдНЧЯпACЕФжаЕудкзјБъдЕуЃЌвЛБпABгыxжсЦНааЧвAB=2ЃЌШєЕуAЕФзјБъЮЊЃЈaЃЌbЃЉЃЌдђЕуDЕФзјБъЮЊ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЭЙЫФБпаЮABCDжаЃЌЁЯA=ЁЯC=90ЁуЃЎ


ЃЈ1ЃЉШчЭМ1ЃЌШєDEЦНЗжЁЯADCЃЌBFЦНЗжЁЯABCЕФСкВЙНЧЃЌХаЖЯDEгыBFЮЛжУЙиЯЕВЂжЄУїЃЎ
ЃЈ2ЃЉШчЭМ2ЃЌШєBFЁЂDEЗжБ№ЦНЗжЁЯABCЁЂЁЯADCЕФСкВЙНЧЃЌХаЖЯDEгыBFЮЛжУЙиЯЕВЂжЄУїЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПСНИіаЁзщЭЌЪБДгМзЕиГіЗЂЃЌдШЫйВНааЕНввЕиЃЌМзввСНЕиЯрОр7500УзЃЌЕквЛзщЕФВНааЫйЖШЪЧЕкЖўзщЕФ1.2БЖЃЌВЂЧвБШЕкЖўзщдч15ЗжжгЕНДяввЕиЃЎЩшЕкЖўзщЕФВНааЫйЖШЮЊxЧЇУз/аЁЪБЃЌИљОнЬтвтПЩСаЗНГЬЪЧЃЈЁЁЁЁЃЉ
A.![]() Љ
Љ ![]() =15
=15
B.![]() Љ
Љ ![]() =
= ![]()
C.![]() Љ
Љ ![]() =15
=15
D.![]() Љ
Љ ![]() =
= ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌOЮЊжБЯпABЩЯвЛЕуЃЌЁЯAOCЃН50ЁуЃЌODЦНЗжЁЯAOCЃЌЁЯDOEЃН90Ёу.
(1)ЧыФуЪ§вЛЪ§ЃЌЭМжагаЖрЩйИіаЁгкЦННЧЕФНЧЃЛ
(2)ЧѓГіЁЯBODЕФЖШЪ§ЃЛ
(3)ЧыЭЈЙ§МЦЫуЫЕУїOEЪЧЗёЦНЗжЁЯBOC.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ|a+b|+|a-b|-2b=0ЃЌдкЪ§жсЩЯИјГіЙигкaЃЌbЕФЫФжжЮЛжУЙиЯЕШчЭМЫљЪОЃЌдђПЩФмГЩСЂЕФгаЃЈЁЁЁЁЃЉ
![]()
A. 1жж B. 2жж C. 3жж D. 4жж
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABЪЧЁбOЕФжБОЖЃЌACЪЧЁбOЕФЯвЃЌЙ§ЕуCЕФЧаЯпНЛABЕФбгГЄЯпгкЕуDЃЌШєЁЯA=ЁЯDЃЌCD=3ЃЌдђЭМжавѕгАВПЗжЕФУцЛ§ЮЊ ЃЎ 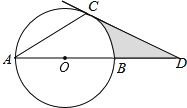
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌдкГЄЗНаЮ![]() жаЃЌAB=4cmЃЌBC=6cmЃЌЕу
жаЃЌAB=4cmЃЌBC=6cmЃЌЕу![]() ЮЊ
ЮЊ![]() жаЕуЃЌШчЙћЕу
жаЕуЃЌШчЙћЕу![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯвдУПУы2cmЕФЫйЖШгЩЕу
ЩЯвдУПУы2cmЕФЫйЖШгЩЕу![]() ЯђЕу
ЯђЕу![]() дЫЖЏЃЌЭЌЪБЃЌЕу
дЫЖЏЃЌЭЌЪБЃЌЕу![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯгЩЕу
ЩЯгЩЕу![]() ЯђЕу
ЯђЕу![]() дЫЖЏЃЎЩшЕу
дЫЖЏЃЎЩшЕу![]() дЫЖЏЪБМфЮЊ
дЫЖЏЪБМфЮЊ![]() УыЃЌШєФГвЛЪБПЬЁїBPEгыЁїCQPШЋЕШЃЌЧѓДЫЪБ
УыЃЌШєФГвЛЪБПЬЁїBPEгыЁїCQPШЋЕШЃЌЧѓДЫЪБ![]() ЕФжЕМАЕу
ЕФжЕМАЕу![]() ЕФдЫЖЏЫйЖШЃЎ
ЕФдЫЖЏЫйЖШЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com