Question

【题目】如图，已知△ABC，按如下步骤作图： ①分别以A，C为圆心，大于 AC的长为半径画弧，两弧交于P，Q两点；
②作直线PQ，分别交AB，AC于点E，D，连接CE；
③过C作CF∥AB交PQ于点F，连接AF．

（1）求证：△AED≌△CFD；
（2）求证：四边形AECF是菱形．

Answer 1

【答案】
（1）证明：由作图知：PQ为线段AC的垂直平分线，

∴AE=CE，AD=CD，

∵CF∥AB

∴∠EAC=∠FCA，∠CFD=∠AED，

在△AED与△CFD中，

，

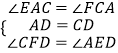∴△AED≌△CFD

（2）解：∵△AED≌△CFD，

∴AE=CF，

∵EF为线段AC的垂直平分线，

∴EC=EA，FC=FA，

∴EC=EA=FC=FA，

∴四边形AECF为菱形

【解析】（1）由作图知：PQ为线段AC的垂直平分线，从而得到AE=CE，AD=CD，然后根据CF∥AB得到∠EAC=∠FCA，∠CFD=∠AED，利用ASA证得两三角形全等即可；（2）根据全等得到AE=CF，然后根据EF为线段AC的垂直平分线，得到EC=EA，FC=FA，从而得到EC=EA=FC=FA，利用四边相等的四边形是菱形判定四边形AECF为菱形．
【考点精析】解答此题的关键在于理解菱形的判定方法的相关知识，掌握任意一个四边形，四边相等成菱形；四边形的对角线，垂直互分是菱形．已知平行四边形，邻边相等叫菱形；两对角线若垂直，顺理成章为菱形．