
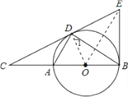
【题目】如图,点D为⊙O上的一点,点C在直径BA的延长线上,并且∠CDA=∠CBD.

(1)求证:CD是⊙O的切线;
(2)过点B作O的切线,交CD的延长线于点E,若BC=12,tan∠CDA=![]() ,求BE的长.
,求BE的长.
【答案】(1)证明见解析;(2) BE的长为5.
【解析】试题分析: (1)如图,连接OD.欲证明CD是⊙O的切线,只需证明CD⊥OA即可.(2)通过相似三角形△EBC∽△ODC的对应边成比例列出关于BE的方程,通过解方程来求线段BE的长度即可.
试题解析:
(1)证明:连OD,OE,如图,∵AB为直径,∴∠ADB=90°,即∠ADO+∠1=90°,
又∵∠CDA=∠CBD,而∠CBD=∠1,∴∠1=∠CDA,∴∠CDA+∠ADO=90°,即∠CDO=90°,∴CD是⊙O的切线;
(2)解:∵EB为⊙O的切线,∴ED=EB,OE⊥DB,∴∠ABD+∠DBE=90°,∠OEB+∠DBE=90°,
∴∠ABD=∠OEB,∴∠CDA=∠OEB.而tan∠CDA=![]() ,∴tan∠OEB=
,∴tan∠OEB=![]() =
=![]() ,
,
∵Rt△CDO∽Rt△CBE,(1)证明:连OD,OE,如图,
∵AB为直径,∴∠ADB=90°,即∠ADO+∠1=90°,又∵∠CDA=∠CBD,而∠CBD=∠1,∴∠1=∠CDA,
∴∠CDA+∠ADO=90°,即∠CDO=90°,∴CD是⊙O的切线;∴![]()
![]() ,∴CD=
,∴CD=![]() ×12=8,
×12=8,
在Rt△CBE中,设BE=x,∴(x+8)2=x2+122,解得x=5.即BE的长为5.


科目:初中数学 来源: 题型:
【题目】现在网购越来越多地成为人们的一种消费方式,在2016年的“双11”网上促销活动中天猫和淘宝的支付交易额突破120700000000元,将120700000000用科学记数法表示为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮从家步行到公交车站台,等公交车去学校.图中的折线表示小亮的行程s(km)与所花时间t(min)之间的函数关系.下列说法错误的是( ) 
A.他离家8km共用了30min
B.他等公交车时间为6min
C.他步行的速度是100m/min
D.公交车的速度是350m/min
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解学生对篮球、足球、排球、羽毛球、乒乓球这五种球类运动的喜爱情况,随机抽取一部分学生进行问卷调查,统计整理并绘制了以下两幅不完整的统计图:

请根据以上统计图提供的信息,解答下列问题:
(1)共抽取_____名学生进行问卷调查;
(2)补全条形统计图,求出扇形统计图中“篮球”所对应的圆心角的度数;
(3)该校共有2500名学生,请估计全校学生喜欢足球运动的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七年级下学期数学教材第155页的问题3:某地区有500万电视观众,要想了解他们对新闻、体育、动画、娱乐、戏曲五类节目的喜爱情况,抽取一个容量为1000的样本进行调查.小波同学根据各年龄段实际人口比例分配抽取的人数制成如下条形图 ;

请你帮助小波再制作一个反映该地区实际人口比例情况的扇形图,并写出每一部分扇形圆心角的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com