【题目】适合下列条件的△ABC中, 直角三角形的个数为
①
②
，∠A=45°;③∠A=32°, ∠B=58°；
④
⑤
⑥
⑦
⑹
A. 2个 B. 3个 C. 4个 D. 5个
【答案】C
【解析】根据勾股定理的逆定理，可分别求出各边的平方，然后计算判断：
，故①不能构成直角三角形；
当a=6，∠A=45°时，②不足以判定该三角形是直角三角形；
根据直角三角形的两锐角互余，可由∠A+∠B=90°，可知③是直角三角形；
根据72=49，242=576，252=625，可知72+242=252，故④能够成直角三角形；
由三角形的三边关系，2+2=4可知⑤不能构成三角形；
令a=3x，b=4x，c=5x，可知a2+b2=c2，故⑥能够成直角三角形；
根据三角形的内角和可知⑦不等构成直角三角形；
由a2=5，b2=20，c2=25，可知a2+b2=c2，故⑧能够成直角三角形.
故选：C.
科目：初中数学 来源： 题型：
【题目】在△ABC和△DEF中，已知AB=DE，∠A=∠D，若要得到△ABC≌△DEF，则还要补充一个条件，在下列补充方法：①AC=DF；②∠B=∠E；③∠B=∠F；④∠C=∠F ⑤BC=EF中，则错误结论的序号是__________ .
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB是圆O的直径，CD是圆O的一条弦，且CD⊥AB于点E．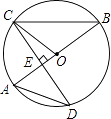 
（1）若∠A=48°，求∠OCE的度数；
（2）若CD=4 
，AE=2，求圆O的半径．
查看答案和解析>>
科目：初中数学 来源： 题型：
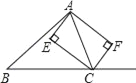
【题目】已知：如图，CE、CF分别是△ABC的内外角平分线，过点A作CE、CF的垂线，垂足分别为E、F．
（1）求证：四边形AECF是矩形；
（2）当△ABC满足什么条件时，四边形AECF是正方形？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，P是抛物线y=2（x﹣2）2对称轴上的一个动点，直线x=t平行y轴，分别与y=x、抛物线交于点A，B．若△ABP是以点A或点B为直角顶点的等腰直角三角形，求满足条件的t的值，则t= ．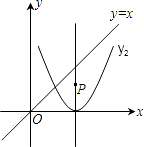 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】计算：
（1）0﹣（﹣2）
（2）（+10）+（﹣14）
（3）5.6+（﹣0.9）+4.4+（﹣8.1）
（4）1﹣
+
﹣
+
（5）（﹣0.5）﹣（﹣3
）+2.75﹣（+7
）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】九（1）班数学兴趣小组经过市场调查，整理出某种商品在第x（1≤x≤90）天的售价与销量的相关信息如下表：
时间x（天） | 1≤x＜50 | 50≤x≤90 |
售价（元/件） | x+40 | 90 |
每天销量（件） | 200﹣2x | |
已知该商品的进价为每件30元，设销售该商品的每天利润为y元．
（1）求出y与x的函数关系式；
（2）问销售该商品第几天时，当天销售利润最大，最大利润是多少？
（3）该商品在销售过程中，共有多少天每天销售利润不低于4800元？请直接写出结果．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我国邮政部门规定：国内平信
克以内（包括克）每
克需贴邮票
元，不足克重的以克计算；超过克的，超过部分每克需加贴
元，不足克的以克计算．
寄一封重
克的国内平信，需贴邮票多少元？
某人寄一封国内平信贴了
元邮票，此信重约多少克？
有
人参加一次数学竞赛，每份答卷重
克，每个信封重
克，将这份答卷分装两个信封寄出，怎样装才能使所贴邮票金额最少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知一次函数y=kx+b与y=﹣2kx（k≠0）的图象相交于点P（1，﹣4）．
（1）求k、b的值；
（2）Q点（m，n）在函数y=kx+b的图象上．
①求2n﹣4m+9的值；
②若一次函数y=x的图象经过点Q，求点Q的坐标．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com