
【题目】如图,点A,B,C,D在⊙O上,点O在∠D的内部,四边形OABC为平行四边形,则∠OAD+∠OCD=°. 
【答案】60
【解析】解:∵四边形OABC为平行四边形, ∴∠AOC=∠B,∠OAB=∠OCB,∠OAB+∠B=180°.
∵四边形ABCD是圆的内接四边形,
∴∠D+∠B=180°.
又∠D= ![]() ∠AOC,
∠AOC,
∴3∠D=180°,
解得∠D=60°.
∴∠OAB=∠OCB=180°﹣∠B=60°.
∴∠OAD+∠OCD=360°﹣(∠D+∠B+∠OAB+∠OCB)=360°﹣(60°+120°+60°+60°)=60°.
故答案为:60.
利用四边形OABC为平行四边形,可得∠AOC=∠B,∠OAB=∠OCB,∠OAB+∠B=180°.利用四边形ABCD是圆的内接四边形,可得∠D+∠B=180°.利用同弧所对的圆周角和圆心角可得∠D= ![]() ∠AOC,求出∠D=60°,进而即可得出.
∠AOC,求出∠D=60°,进而即可得出.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图, ![]() ,射线
,射线![]() ,且
,且![]() ,
, ![]() ,点
,点![]() 是线段
是线段![]() (不与点
(不与点![]() 、
、![]() 重合)上的动点,过点
重合)上的动点,过点![]() 作
作![]() 交射线
交射线![]() 于点
于点![]() ,连结
,连结![]() .
.
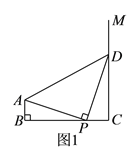
(![]() )如图
)如图![]() ,若
,若![]() ,求证:
,求证: ![]() ≌
≌![]() .
.
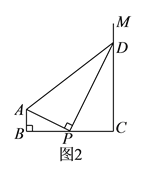
(![]() )如图
)如图![]() ,若
,若![]() 平分
平分![]() ,试猜测
,试猜测![]() 和
和![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
(![]() )若
)若![]() 是等腰三角形,作点
是等腰三角形,作点![]() 关于
关于![]() 的对称点
的对称点![]() ,连结
,连结![]() ,则
,则![]() __________.(请直接写出答案)
__________.(请直接写出答案)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,AB=AC=12厘米,∠B=∠C,BC=8厘米,点D为AB的中点.如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为v厘米/秒,则当△BPD与△CQP全等时,v的值为________厘米/秒.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知下面四个图形中,AB∥CD,探究四个图形中,∠APC与∠PAB,∠PCD的数量关系.
(1)图①中,∠APC与∠PAB,∠PCD的关系是__________________;
(2)图②中,∠APC与∠PAB,∠PCD的关系是__________________;
(3)请你在图③和图④中任选一个,说明∠APC与∠PAB,∠PCD的关系,并加以证明



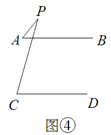
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知小敏家距学校5km,小飞家距小敏家3km.若小飞家距学校距离为xkm,则x满足( )
A.x=2B.2≤x≤8C.2≤x≤5D.2<x<8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件50元,售价为每件60元,每个月可卖出200件;如果每件商品的售价每上涨1元,则每个月少卖10件.设每件商品的售价上涨x元(x为正整数),每个月的销售利润为y元.
(1)求y与x的函数关系式;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
(3)若每个月的利润不低于2160元,售价应在什么范围?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com