
【题目】如图,直线y=kx+b与双曲线y=![]() 相交于点A,B,与x轴相交于点C,矩形DEFG的端点D在直线AB上,E,F在x轴上,点G在双曲线上,若DE=
相交于点A,B,与x轴相交于点C,矩形DEFG的端点D在直线AB上,E,F在x轴上,点G在双曲线上,若DE=![]() ,CE=2,点A的横坐标是1.
,CE=2,点A的横坐标是1.
(1)求点A,G的坐标;
(2)求直线AB的解析式.

【答案】(1)(2,![]() )(2)y=
)(2)y=![]() x+
x+![]() .
.
【解析】
试题分析:(1)由矩形的性质结合DE=![]() ,可知点G的纵坐标为
,可知点G的纵坐标为![]() ,分别令双曲线y=
,分别令双曲线y=![]() 中x=1、y=
中x=1、y=![]() ,即可求出点A、G的坐标;
,即可求出点A、G的坐标;
(2)分别令直线y=kx+b中y=0、y=![]() ,求出点C、E的横坐标,结合线段CE=2即可得出关于k的一元一次方程,解方程即可得出k值,将k值和点A的坐标代入到直线y=kx+b中得出关于b的一元一次方程,解方程即可得出结论.
,求出点C、E的横坐标,结合线段CE=2即可得出关于k的一元一次方程,解方程即可得出k值,将k值和点A的坐标代入到直线y=kx+b中得出关于b的一元一次方程,解方程即可得出结论.
试题解析:(1)∵DE=![]() ,且四边形DEFG为矩形,
,且四边形DEFG为矩形,
∴GF=DE=![]() .
.
令双曲线y=![]() 中x=1,则y=
中x=1,则y=![]() =3,
=3,
∴点A的坐标为(1,3);
令双曲线y=![]() 中y=
中y=![]() ,则
,则![]() =
=![]() ,解得:x=2,
,解得:x=2,
∴点G的坐标为(2,![]() ).
).
(2)令直线y=kx+b中y=![]() ,则
,则![]() =kx+b,解得:x=
=kx+b,解得:x=![]() ,
,
即点D的坐标为(![]() ,
,![]() ),点E的坐标为(
),点E的坐标为(![]() ,0);
,0);
令直线y=kx+b中y=0,则0=kx+b,解得:x=﹣![]() ,
,
即点C的坐标为(﹣![]() ,0).
,0).
∵CE=![]() ﹣(﹣
﹣(﹣![]() )=2,
)=2,
∴![]() =2k,解得:k=
=2k,解得:k=![]() ,
,
∴直线AB的解析式为y=![]() x+b,
x+b,
∵点A(1,3)在直线AB上,
∴3=![]() +b,解得:b=
+b,解得:b=![]() ,
,
∴直线AB的解析式为y=![]() x+
x+![]() .
.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】已知一次函数y=2x+4
(1)在如图所示的平面直角坐标系中,画出函数的图象;

2)求图象与x轴的交点A的坐标,与y轴交点B的坐标;
(3)在(2)的条件下,求出△AOB的面积;
(4)利用图象直接写出:当y<0时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长沙某抗战纪念馆馆长联系某中学,选择18名青少年志愿者在同日参与活动,年龄如表所示:这18名志愿者年龄的众数和中位数分别是( )
年龄(单位:岁) | 12 | 13 | 14 | 15 |
人数 | 3 | 5 | 6 | 4 |
A.13,14B.14,14C.14,13D.14,15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一道题,当a=2,b=﹣2时,求多项式:
3a3b3﹣ ![]() a2b+b2﹣3(a3b3﹣
a2b+b2﹣3(a3b3﹣ ![]() a2b﹣b2)﹣2b2﹣3的值,马虎做题时把a=2错抄成a=﹣2,王真没抄错题,但他们做出的结果却都一样,你知道这是怎么回事吗?说明理由.
a2b﹣b2)﹣2b2﹣3的值,马虎做题时把a=2错抄成a=﹣2,王真没抄错题,但他们做出的结果却都一样,你知道这是怎么回事吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
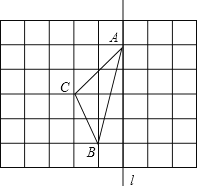
【题目】如图,在长度为1个单位长度的小正方形组成的正方形网格中,点A、B、C在小正方形的顶点上.
(1)在图中画出与关于直线![]() 成轴对称的△A′B′C′;
成轴对称的△A′B′C′;
(2)线段CC′被直线![]() ;
;
(3)△ABC的面积为 ;
(4)在直线![]() 上找一点P,使PB+PC的长最短.
上找一点P,使PB+PC的长最短.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com