
 在平面直角坐标系xOy中,抛物线y=$\frac{1}{2}a{x^2}$+2x-a+1与y轴交于C点,与x轴交于A,B两点(点A在点B左侧),且点A的横坐标为-1.
在平面直角坐标系xOy中,抛物线y=$\frac{1}{2}a{x^2}$+2x-a+1与y轴交于C点,与x轴交于A,B两点(点A在点B左侧),且点A的横坐标为-1.分析 (1)把A(-1,0)代入抛物线解析式,列出关于a的一元一次方程,通过解该方程求得a的值;
(2)根据(1)中抛物线解析式求得顶点P的坐标,然后由关于原点对称的两点的横、纵坐标均互为相反数来求点P′的坐标;
(3)由点P、P′的坐标求得直线PP′的解析式,然后根据平移的性质并结合图形进行答题.
解答 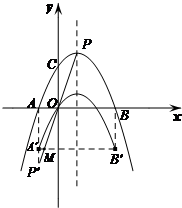 解:
解:
(1)∵A(-1,0)在抛物线$y=\frac{1}{2}a{x^2}+2x-a+1$上,
∴$\frac{1}{2}a-2x-a+1=0$,
∴解得a=-2.
(2)∴抛物线表达式为y=-x2+2x+3.
∴抛物线y=-x2+2x+3的顶点P的坐标为(1,4).
∵点P关于原点的对称点为P',
∴P'的坐标为(-1,-4).
(3)直线PP'的表达式为y=4x,
图象向下平移3个单位后,A'的坐标为(-1,-3),B'的坐标为(3,-3),
若图象G与直线PP'无交点,则B'要左移到M及左边,
令y=-3代入PP',则$x=-\frac{3}{4}$,M的坐标为$({-\frac{3}{4},-3})$,
∴$B'M=3-({-\frac{3}{4}})=\frac{15}{4}$,
∴$m>\frac{15}{4}$.
点评 本题考查了二次函数图象与几何变换,待定系数法求二次函数解析式以及二次函数图象上点的坐标特征.此题中的点A的坐标是隐含在题中的一个已知条件.


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{3}{8}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
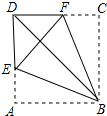 如图,将正方形纸片ABCD折叠,使边AB、CB均落在对角线BD上,得折痕BE、BF,则∠EBF的大小为( )
如图,将正方形纸片ABCD折叠,使边AB、CB均落在对角线BD上,得折痕BE、BF,则∠EBF的大小为( )| A. | 60° | B. | 45° | C. | 30° | D. | 15° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com