
| A. | 4 | B. | 6 | C. | 2 | D. | 8 |
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
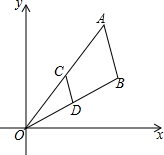 如图,线段AB两个端点的坐标分别为A(6,8),B(7,4),以原点为位似中心,在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD.则端点C的坐标为( )
如图,线段AB两个端点的坐标分别为A(6,8),B(7,4),以原点为位似中心,在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD.则端点C的坐标为( )| A. | (3,3) | B. | (4,3) | C. | (3,4) | D. | ($\frac{7}{2}$,2) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
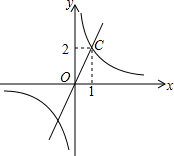 反比例函数y﹦$\frac{k}{x}$和正比例函数y﹦mx的图象如图所示.由此可以得到方程$\frac{k}{x}$﹦mx的实数根为( )
反比例函数y﹦$\frac{k}{x}$和正比例函数y﹦mx的图象如图所示.由此可以得到方程$\frac{k}{x}$﹦mx的实数根为( )| A. | x=1 | B. | x=2 | C. | x1=1,x2=-1 | D. | x1=1,x2=-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
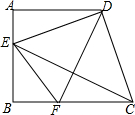 如图,已知在梯形ABCD中,AD∥BC,∠A=90°,AB=AD,点E在边AB上,且DE⊥CD,DF平分∠EDC,交BC于点F,联结CE、EF.
如图,已知在梯形ABCD中,AD∥BC,∠A=90°,AB=AD,点E在边AB上,且DE⊥CD,DF平分∠EDC,交BC于点F,联结CE、EF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
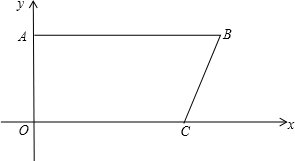
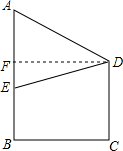 如图,某地为响应市政府“形象重于生命”的号召,在甲建筑物上从点A到点E挂一长为30米的宣传条幅,在乙建筑物的顶部D点测得条幅顶端A点的仰角为40°,测得条幅底端E的俯角为26°,求甲、乙两建筑物的水平距离BC的长(精确到0.1米).
如图,某地为响应市政府“形象重于生命”的号召,在甲建筑物上从点A到点E挂一长为30米的宣传条幅,在乙建筑物的顶部D点测得条幅顶端A点的仰角为40°,测得条幅底端E的俯角为26°,求甲、乙两建筑物的水平距离BC的长(精确到0.1米).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
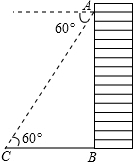 已知在离地面30米的高楼窗台A处测得地面花坛中心标志物C的俯角为60°,那么这一标志物C离此栋楼房的地面距离BC为10$\sqrt{3}$米.
已知在离地面30米的高楼窗台A处测得地面花坛中心标志物C的俯角为60°,那么这一标志物C离此栋楼房的地面距离BC为10$\sqrt{3}$米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com