
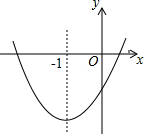
 已知二次函数y=ax2+bx+c的图象如图所示(虚线部分是对称轴);则下列结论:
已知二次函数y=ax2+bx+c的图象如图所示(虚线部分是对称轴);则下列结论:| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
分析 根据抛物线与x轴的交点情况,抛物线的开口方向,对称轴及与y轴的交点,当x=-2或x=1时的函数值,逐一判断.
解答 解:①抛物线开口向上,得:a>0;
抛物线的对称轴为x=-$\frac{b}{2a}$=-1,b=2a,故b>0;
抛物线交y轴于负半轴,得:c<0;
所以abc<0;
故①错误,②正确;
③抛物线与x轴有两个不同的交点,则△=b2-4ac>0,故4ac-b2<0,故③正确;
④当x=1时,y>0,即a+b+c>0,故④错误;
⑤当x=-2时,y<0,即4a-2b+c<0,故4a+c<2b,则⑤正确;
⑥根据②可将抛物线的解析式化为:y=ax2+2ax+c(a≠0);
由函数的图象知:当x=2时,y>0;即4a+4a+c=8a+c>0,故⑥正确;
故正确的结论有4个.
故选:B.
点评 此题主要考查了图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换,根的判别式的熟练运用.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案科目:初中数学 来源: 题型:解答题
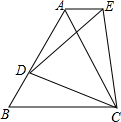 如图,等边△ABC中,D是AB边上的动点,以CD为一边向上作等边△EDC,连接AE.(1)求证:AE∥BC.
如图,等边△ABC中,D是AB边上的动点,以CD为一边向上作等边△EDC,连接AE.(1)求证:AE∥BC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
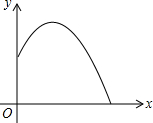 某公园一喷水池喷水时水流的路线呈抛物线(如图).若喷水时水流的高度y(m)与水平距离x(m)之间的函数关系式是y=-x2+2x+1.25,则水池在喷水过程中水流的最大高度为( )
某公园一喷水池喷水时水流的路线呈抛物线(如图).若喷水时水流的高度y(m)与水平距离x(m)之间的函数关系式是y=-x2+2x+1.25,则水池在喷水过程中水流的最大高度为( )| A. | 1.25米 | B. | 2.25米 | C. | 2.5米 | D. | 3米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
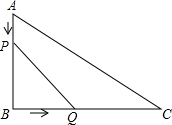 如图,在Rt△ABC中,∠B=90°,AB=6cm,BC=12cm,点P从点A出发,沿AB边向点B以1cm/s的速度移动,同时点Q从点B出发沿BC边向点C以2cm/s的速度移动,如果P,Q两点同时出发,分别到达B,C两点后就停止移动.
如图,在Rt△ABC中,∠B=90°,AB=6cm,BC=12cm,点P从点A出发,沿AB边向点B以1cm/s的速度移动,同时点Q从点B出发沿BC边向点C以2cm/s的速度移动,如果P,Q两点同时出发,分别到达B,C两点后就停止移动.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
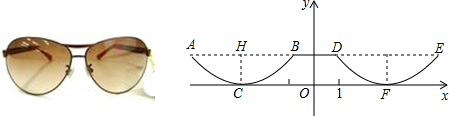
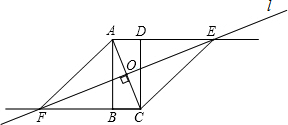 如图,四边形ABCD是矩形,直线l垂直平分线段AC,垂足为O,直线l分别与线段AD、CB的延长线交于点E、F.试判定四边形AFCE的形状,并说明理由.
如图,四边形ABCD是矩形,直线l垂直平分线段AC,垂足为O,直线l分别与线段AD、CB的延长线交于点E、F.试判定四边形AFCE的形状,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com