
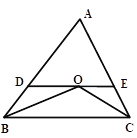
【题目】如图,∠ABC和∠ACB的平分线交于点O,DE经过点O且平行于BC,分别与AB,AC交于点D、E。
(1)如图1,若∠ABC=50°,∠ACB=60°,求∠BOC的度数;
(2)如图1,若∠ABC=α°,∠ACB=β°,用含α、β的式子表示∠BOC的度数;
(3)探究:如图空白图,在第(2)问的条件下,若∠ABC和∠ACB的邻补角的平分线交于点O,其他条件不变,请画出相应图形,并用含α、β的式子表示∠BOC的度数。
【答案】(1)125°;(2)![]() ;(3)
;(3)![]()
【解析】整体分析:
(1)根据角平分线的性质和平行线的性质,求出∠BOD+∠COE的度数即可;(2)与(1)的方法类似,用α,β表示∠BOD+∠COE的度数;(3)根据题意,画出图形,用角平分线的定义和三角形的内角和定理求解.
解:(1)∵∠ABC和∠ACB的平分线交于点O,
∴∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,
∠ACB,
∵∠ABC=50°,∠ACB=60°,
∴∠OBC+∠OCB=![]() (∠ABC+∠ACB)=55°.
(∠ABC+∠ACB)=55°.
∵DE∥BC,
∴∠OBC=∠BOD,∠OCB=∠COE,
∴∠BOC=180°-(∠BOD+∠COE)
=180°-(∠OBC+∠OCB)
=180°-55°=125°.
(2)∵∠ABC和∠ACB的平分线交于点O,
∴∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,
∠ACB,
∵∠ABC=α°,∠ACB=β°,
∴∠OBC+∠OCB=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() (α+β).
(α+β).
∵DE∥BC,
∴∠OBC=∠BOD,∠OCB=∠COE,
∴∠BOC=180°-(∠BOD+∠COE)
=180°-(∠OBC+∠OCB)
=180°-![]() (α+β).
(α+β).
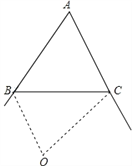
(3)∵BO,CO分别为△ABC的外角的平分线,
∴∠OBC=90°-![]() α,∠OCB=90°-
α,∠OCB=90°-![]() β,
β,
∴∠BOC=180°-(∠OBC+∠OCB)
=180°-(90°-![]() α+90°-
α+90°-![]() β)
β)
=![]() (α+β).
(α+β).


科目:初中数学 来源: 题型:
【题目】(1) 若方程4x-1=3x+1和2m+x=1的解相同.求m![]() 的值.
的值.
(2)在公式S=![]() (a+b)h中,已知S=120,b=18,h=8.求a的值.
(a+b)h中,已知S=120,b=18,h=8.求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
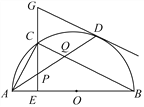
【题目】如图,在⊙O中,AB是直径,点D是⊙O上一点,点C是![]() 的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE,CB于点P,Q,连接AC,关于下列结论:①∠BAD=∠ABC;②GP=GD;③点P是△ACQ的外心,其中结论正确的是________(只需填写序号).
的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE,CB于点P,Q,连接AC,关于下列结论:①∠BAD=∠ABC;②GP=GD;③点P是△ACQ的外心,其中结论正确的是________(只需填写序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰Rt△ABC中,∠ABC=90°,AB=CB=2,点D为AC的中点,点E,F分别是线段AB,CB上的动点,且∠EDF=90°,若ED的长为m,则△BEF的周长是______(用含m的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】坐火车从上海到娄底,高铁G1329次列车比快车K575次列车少需要9小时,已知上海到娄底的铁路长约1260千米,G1329的平均速度是K575的2.5倍.
(1)求K575的平均速度;
(2)高铁G1329从上海到娄底只需几小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为给研究制定《中考改革实施方案》提出合理化建议,教研人员对九年级学生进行了随机抽样调查,要求被抽查的学生从物理、化学、政治、历史、生物和地理这六个选考科目中,挑选出一科作为自己的首选科目,将调查数据汇总整理后,绘制出了如图的两幅不完整的统计图,请你根据图中信息解答下列问题:
(1)被抽查的学生共有多少人?
(2)将折线统计图补充完整;
(3)我市现有九年级学生约40000人,请你估计首选科目是物理的人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国倡导的“一带一路”建设将促进我国与世界各国的互利合作.根据规划,“一带一路”地区覆盖总人口约为4400000000人,这个数用科学记数法表示为 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题是真命题的是( )
A.内错角相等
B.平面内,过一点有且只有一条直线与已知直线垂直
C.相等的角是对顶角
D.过一点有且只有一条直线与已知直线平行
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国古代数学家们对于勾股定理的发现和证明,在世界数学史上具有独特的贡献和地位,体现了数学研究中的继承和发展.现用4个全等的直角三角形拼成如图所示“弦图”.Rt△ABC中,∠ACB=90°,若![]() ,请你利用这个图形解决下列问题:
,请你利用这个图形解决下列问题:
(1)试说明![]() ;
;
(2)如果大正方形的面积是10,小正方形的面积是2,求![]() 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com