
����Ŀ���Ķ����ϣ�һ�������µ�ʽ![]() ��1������������Щ����ʵ������ʹ�����������磺x��2��y��2ʱ��
��1������������Щ����ʵ������ʹ�����������磺x��2��y��2ʱ��![]() ��1���������dz�(2��2)��ʹ
��1���������dz�(2��2)��ʹ![]() ��1��������������������������������⣺
��1��������������������������������⣺
��1������(![]() ��4)��(1��1)�У�ʹ
��4)��(1��1)�У�ʹ![]() ��1���������������������� ����
��1���������������������� ����
��2����(5��t��5+t)��ʹ![]() ��1����������������������t��ֵ��
��1����������������������t��ֵ��
��3����(m��n)��ʹ![]() ��1����������������������a��b+m��b��c+n�������ʽ��a��c��2��12��a��b����b��c������Сֵ��
��1����������������������a��b+m��b��c+n�������ʽ��a��c��2��12��a��b����b��c������Сֵ��
���𰸡���1��(![]() ��4)����2����
��4)����2����![]() ����3����36
����3����36
��������
��1���������ж��彫���ԣ�![]() ��4������1��1���ֱ����㼴�ɣ�
��4������1��1���ֱ����㼴�ɣ�
��2����������ù���t �ķ�ʽ���̣��ⷽ�̼��ɣ�
��3��������֪�������Ƚ�m��n�ú�a��b��c��ʽ�ӱ�ʾ�������ٸ�������ó�����m��n�ĵ�ʽ��Ȼ��ɵù���a��b��c�ĵ�ʽ���Ӷ��ɶ������Ĵ���ʽ�䷽�������ֵ��
�⣺��1����![]() +
+![]() ��
��![]() +
+![]() ��1
��1
����![]() ��4����ʹ
��4����ʹ![]() ��1��������������������
��1��������������������
��![]() +
+![]() ��2��1
��2��1
����1��1������ʹ![]() ��1��������������������
��1��������������������
�ʴ�Ϊ����![]() ��4����
��4����
��2������5��t��5+t����ʹ![]() ��1��������������������
��1��������������������
��![]() +
+![]() ��1
��1
��5+t+5��t��25��t2
��t����![]()
�����飬t����![]() ��ԭ���̵Ľ�
��ԭ���̵Ľ�
��t��ֵΪ��![]() ��
��
��3����a��b+m��b��c+n
��m��a��b��n��b��c
������ã�![]() +
+![]() ��1
��1
![]() +
+![]() ��1
��1
��b��c+a��b����a��b����b��c��
��a��c����a��b����b��c��
����a��c��2��12��a��b����b��c��
����a��c��2��12��a��c��
����a��c��6��2��36
����a��c��6��2��0
����a��c��6��2��36����36
������ʽ��a��c��2��12��a��b����b��c������СֵΪ��36��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
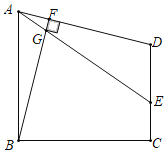
����Ŀ�����ı���ABCD�У���ABC����DCB��90����AB��BC.����B��BF��AD������Ϊ��F��
��1����֤����DAB����FBC��
��2����EΪ�߶�CD�ϵ�һ�㣬����AE��BF��G������BAE+2��EAD��90����AG��1��AB��5�����߶�CD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˴ٽ�ѧ����������չ��ijУ��֯��չ�����Ż���ֱ������������ࡢ�����ࡢ��ѧ�༰���������ţ�Ҫ�����˲������ţ�ÿ��ֻ��ѡ��һ���Ϊ�˽�ѧ��ϲ���������Ż��ѧУ����һ�γ������飮�����ռ��������ݣ����Ƴ�����������������ͳ��ͼ�������ͼ���ṩ����Ϣ������������⣺

��1���˴ι������˶����ˣ�
��2������ѧ����������ͳ��ͼ����ռԲ�ĽǵĶ�����
��3���뽫����ͳ��ͼ����������
��4������У��1500��ѧ���������ϲ�����������ŵ�ѧ���ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
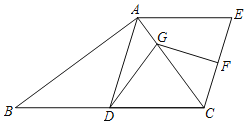
����Ŀ����ͼ����Rt��ABC�У�ADΪб��BC�ϵ����ߣ�AE��BC��CE��AD��EC�Ĵ�ֱƽ����FG��AC��G������DG������ADG��24�������B�Ķ���Ϊ_____�ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�����л���ͳ�Ļ���ijУ�ٰ���ѧ������ѧ�����������������ĿΪ��![]() ����ʫ��
����ʫ��![]() ���δʣ�
���δʣ�![]() �����
�����![]() �����־���������ʽ����������������˫��������
�����־���������ʽ����������������˫��������
��1��С���μ������������������������ȡһ��������Ŀ��ǡ�ó��������־����ĸ����Ƕ��٣�
��2��С���С�����һ��С��μ���˫���������������������ǣ�ͬһС���������Ա�ı�����Ŀ������ͬ����ÿ��ֻ�������ȡһ�Σ���С���С����û�г鵽���������ĸ����Ƕ��٣����û���״ͼ���б��ķ�������˵����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ƽ��ֱ������ϵ�У�B��C���������ֱ�ΪB��0��3����C��0����![]() ������A��x���������ϣ��������BAO��30����
������A��x���������ϣ��������BAO��30����
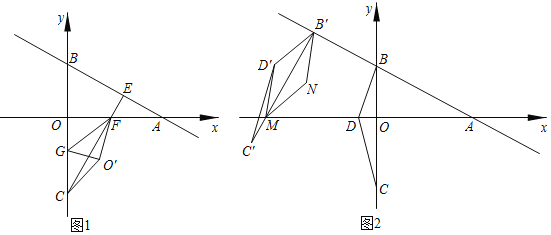
��1������C��CE��AB�ڵ�E����AO�ڵ�F����GΪ�߶�OC��һ���㣬����GF������OFG��FG����ʹ��O����ƽ���ڵĵ�O����������O��C�����߶�OF�ij��Լ��߶�O��C����Сֵ��
��2����ͼ2����D������ΪD����1��0��������BDC�Ƶ�B˳ʱ����ת��ʹ��BC��AB�ڵ�B������ת�����BDC��ֱ��ABƽ�ƣ�ƽ���е���BDC��Ϊ��B��D��C������ֱ��B��C����x�ύ�ڵ�M��NΪƽ��������һ�㣬����B����D����M��NΪ������ı���������ʱ�����M�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪ƽ���ı���OBDC�ĶԽ����ཻ�ڵ�E������O��0��0����B��3��4����C��m��0��������������y=![]() ��k��0����ͼ����B��
��k��0����ͼ����B��
��1�����������Ľ���ʽ��
��2������Eǡ�����ڷ���������y=![]() �ϣ���ƽ���ı���OBDC�������
�ϣ���ƽ���ı���OBDC�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������ƽ�ȫ������ij����ȥ�깺��A��B���ֽ����������ɼ������˽⣬B�ֽ������ĵĵ�����A�ֽ������ĵ�1��5������7200Ԫ����A�ֽ������ı���5400Ԫ����B�ֽ������Ķ�10����
��1��A��B���ֽ������ĵĵ��۷ֱ��Ƕ���Ԫ��
��2�����������ֽ������ĵĵ��ۺ�ȥ�걣�ֲ��䣬�������ƻ��ٹ���A��B���ֽ������Ĺ�50�����ҷ��ò�����21000Ԫ�����ʣ�A�ֽ�����������Ҫ������ټ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У����κ���![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��![]() ����
����![]() ���ڵ�
���ڵ�![]() ����
����![]() ������һ��
������һ��![]() ������
������![]() .
.

��1������κ����ı���ʽ��
��2������![]() ��������
Ϊ��������![]() �Ḻ�����Ϸ���һ�����㣬��
�Ḻ�����Ϸ���һ�����㣬��![]() ��������ֵ��
��������ֵ��
��3�������߶Գ������Ƿ���ڵ�![]() ��ʹ
��ʹ![]() Ϊ���������Σ������ڣ���ֱ��д������
Ϊ���������Σ������ڣ���ֱ��д������![]() ������꣬����������˵������.
������꣬����������˵������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com