
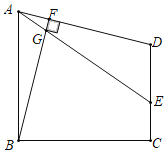
【题目】在四边形ABCD中,∠ABC=∠DCB=90°,AB=BC.过点B作BF⊥AD,垂足为点F,
(1)求证:∠DAB=∠FBC;
(2)点E为线段CD上的一点,连接AE交BF于G,若∠BAE+2∠EAD=90°,AG=1,AB=5,求线段CD的长.
【答案】(1)证明见解析;(2)CD=4.
【解析】
(1)由余角的性质可得结论;
(2)如图,过点A作AH⊥CD,延长BF交AH于M,可证四边形ABCH是正方形,可得AB=CH=5,由“ASA”可证△ABM≌△AHD,△AGF≌△AMF,可得HD=AM,AM=AG=1,即可求解.
证明:(1)∵BF⊥AD,
∴∠AFB=90°,
∴∠DAB+∠ABF=90°,
∵∠ABC=90°,即∠ABF+∠FBC=90°,
∴∠DAB=∠FBC;
(2)如图,过点A作AH⊥CD,垂足为H,延长BF交AH于M,
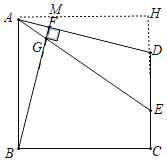
∵AH⊥CD,∠ABC=∠DCB=90°,
∴四边形ABCH是矩形,
又∵AB=BC,
∴矩形ABCH是正方形,
∴AB=CH=5,
∵∠BAE+2∠EAD=90°,∠BAE+∠EAD+∠DAH=90°,∠BAE+∠DAE+∠ABM=90°
∴∠DAH=∠EAD=∠ABM,
又AB=AH,∠BAM=∠H=90°,
∴△ABM≌△HAD(ASA)
∴HD=AM,
∵∠DAE=∠DAH,AF=AF,∠AFG=∠AFM=90°,
∴△AGF≌△AMF(ASA)
∴AM=AG=1,
∴HD=1,
∴CD=CH﹣DH=4.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案科目:初中数学 来源: 题型:
【题目】如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).
(1)把△ABC沿BA方向平移后,点A移到点A1,在网格中画出平移后得到的△A1B1C1;
(2)把△A1B1C1绕点A1按逆时针方向旋转90°,在网格中画出旋转后的△A1B2C2;
(3)如果网格中小正方形的边长为1,求点B经过(1)、(2)变换的路径总长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC中,AB=AC,∠BAC=90°,CD平分∠ACB,BE⊥CD,垂足E在CD的延长线上.请解答下列问题:
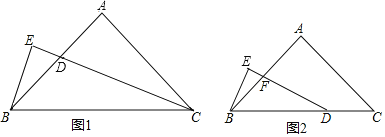
(1)图中与∠DBE相等的角有: ;
(2)直接写出BE和CD的数量关系;
(3)若△ABC的形状、大小不变,直角三角形BEC变为图2中直角三角形BED,∠E=90°,且∠EDB=![]() ∠C,DE与AB相交于点F.试探究线段BE与FD的数量关系,并证明你的结论.
∠C,DE与AB相交于点F.试探究线段BE与FD的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
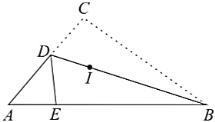
【题目】如图,三角形纸片![]() 中,沿过
中,沿过![]() 点的直线折叠这个三角形,使点
点的直线折叠这个三角形,使点![]() 落在
落在![]() 边上的点
边上的点![]() 处,折痕为
处,折痕为![]() ,则下列结论:
,则下列结论:
①![]() 平分
平分![]() ;
;
②![]() ;
;
③若![]() ,
,![]() ,
,![]() ,则
,则![]() 的周长为7;
的周长为7;
④![]() ;
;
⑤若![]() 平分
平分![]() 与
与![]() 交于点
交于点![]() ,当
,当![]() 时,
时,![]() .其中结论正确的有( )
.其中结论正确的有( )
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
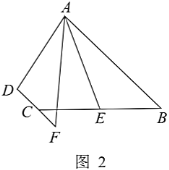
【题目】在四边形![]() 中,
中,![]() ,点
,点![]() 是
是![]() 的中点
的中点
情景引入:
(1)如图1,若![]() 是
是![]() 的平分线,试判断
的平分线,试判断![]() ,
,![]() ,DC之间的等量关系.
,DC之间的等量关系.
解决此问题可以用如下方法:延长![]() 交
交![]() 的延长线于点
的延长线于点![]() ,证明
,证明![]() 得到
得到![]() ,从而把
,从而把![]() ,
,![]() ,
,![]() 转化在一个三角形中即可判断
转化在一个三角形中即可判断![]() ,
,![]() ,
,![]() 之间的等量关系为
之间的等量关系为![]() ,试证明该结论;
,试证明该结论;

问题探究:
(2)如图2,点![]() 是
是![]() 的延长线上一点,连
的延长线上一点,连![]() ,若
,若![]() 恰好是
恰好是![]() 的平分线,试探究
的平分线,试探究![]() ,
,![]() ,
,![]() 之间的等量关系,并证明你的结论.
之间的等量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
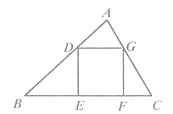
【题目】如图,△ABC中,正方形DEFG的顶点D,G分别在AB,AC上,顶点E,F在BC上.若△ADG、△BED、△CFG的面积分别是1、3、1,则正方形的边长为( )
A. ![]() B.
B. ![]() C. 2 D. 2
C. 2 D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
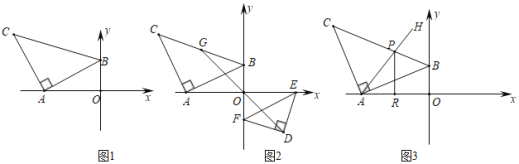
【题目】如图1,将任意一个等腰直角三角板△ABC放至平面直角坐标系xOy中,直角顶点A(a,0)在x轴的负半轴,点B(0,b)在y轴的正半轴,点C落在第二象限,
(1)若![]() =﹣b2+4b﹣4,求C点坐标;
=﹣b2+4b﹣4,求C点坐标;
(2)如图2,再将任意的一个等腰直角三角板△DEF放至平面直角坐标系xOy中,点E在x轴的正半轴上,F在y轴的负半轴上,直角顶点D落在第四象限,设点G为BC的中点,证明:点D,O,G三点刚好在同一条直线上;
(3)已知a=﹣4,b<4.如图3,点O关于直线AB的对称点为点H,AH交线段BC于点P,PR⊥x轴于点R,求△APR的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】圆桌面(桌面中间有一个直径为0.4m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直径为1.2m,桌面离地面1m,若灯泡离地面3m,则地面圆环形阴影的面积是( )

A. 0.324πm2 B. 0.288πm2 C. 1.08πm2 D. 0.72πm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:一般情形下等式![]() =1不成立,但有些特殊实数可以使它成立,例如:x=2,y=2时,
=1不成立,但有些特殊实数可以使它成立,例如:x=2,y=2时,![]() =1成立,我们称(2,2)是使
=1成立,我们称(2,2)是使![]() =1成立的“神奇数对”.请完成下列问题:
=1成立的“神奇数对”.请完成下列问题:
(1)数对(![]() ,4),(1,1)中,使
,4),(1,1)中,使![]() =1成立的“神奇数对”是 ;
=1成立的“神奇数对”是 ;
(2)若(5﹣t,5+t)是使![]() =1成立的“神奇数对”,求t的值;
=1成立的“神奇数对”,求t的值;
(3)若(m,n)是使![]() =1成立的“神奇数对”,且a=b+m,b=c+n,求代数式(a﹣c)2﹣12(a﹣b)(b﹣c)的最小值.
=1成立的“神奇数对”,且a=b+m,b=c+n,求代数式(a﹣c)2﹣12(a﹣b)(b﹣c)的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com