
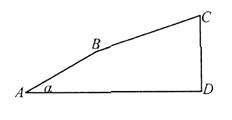
【题目】如图,四边形ABCD中,AD∥BC,DE平分∠ADB,∠BDC=∠BCD.
(1)求证:∠1+∠2=90°;
(2)若∠ABD的平分线与CD的延长线交于F,且∠F=55°,求∠ABC;
(3)若H是BC上一动点,F是BA延长线上一点,FH交BD于M,FG平分∠BFH,交DE于N,交BC于G.当H在BC上运动时(不与B点重合),试判断∠BAD+∠DMH与∠DNG的数量关系,并说明理由.

【答案】(1)证明见解析;(2)70°;(3)∠BAD+∠DMH=2∠DNG,理由见解析
【解析】
(1)由AD∥BC,DE平分∠ADB,得∠ADC+∠BCD=180°,∠BDC=∠BCD,得出∠1+∠2=90°;
(2)由DE平分∠ADB,CD平分∠ABD,四边形ABCD中,AD∥BC,∠F=55°,得出∠ABC=∠ABD+∠DBC=∠ABD+∠ADB,即∠ABC=70°;
(3)在△BMF中,根据角之间的关系∠BMF=180°-∠ABD-∠BFH,得∠GND=180°-∠AED-∠BFG,再根据角之间的关系得∠BAD=∠GND+![]() ∠BFH-∠DBC,再综上得出答案.
∠BFH-∠DBC,再综上得出答案.
(1)∵AD∥BC,
∴∠ADC+∠BCD=180°,
∵DE平分∠ADB,
∴∠BDC=∠BCD,
∴∠ADE=∠EDB,
∠BDC=∠BCD,
∵∠ADC+∠BCD=180°,
∴∠EDB+∠BDC=90°,
∴∠1+∠2=90°;
(2)∵∠FBD+∠BDE=90°﹣∠F=35°,
∵DE平分∠ADB,BF平分∠ABD,
∴∠ADB+∠ABD=2(∠FBD+∠BDE)=70°,
又∵四边形ABCD中,AD∥BC,
∴∠DBC=∠ADB,
∴∠ABC=∠ABD+∠DBC=∠ABD+∠ADB,
即∠ABC=70°;
故答案为:70°
(3)∵在△BMF中,∠BMF=∠DMH=180°﹣∠ABD﹣∠BFH,
又∵∠BAD=180°﹣(∠ABD+∠ADB),
∴∠DMH+∠BAD=(180°﹣∠ABD﹣∠BFH)+(180°﹣∠ABD﹣∠ADB)=360°﹣∠BFH﹣2∠ABD﹣∠ADB,
∴∠DNG=∠FNE=180°﹣![]() ∠BFH﹣∠AED=180°﹣
∠BFH﹣∠AED=180°﹣![]() ∠BFH﹣∠ABD﹣
∠BFH﹣∠ABD﹣![]() ∠ADB=
∠ADB=![]() (∠DMH+∠BAD),
(∠DMH+∠BAD),
即∠BAD+∠DMH=2∠DNG.
故答案为:∠BAD+∠DMH=2∠DNG.


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,BF平分∠ABC,交CD于点E,交AC于点F.若AB=10,BC=6,则CE的长为( )

A. 3B. 4C. 5D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】依据下列解方程![]() 的过程,请在前面的括号内填写变形步骤,在后面的括号内填写变形依据。
的过程,请在前面的括号内填写变形步骤,在后面的括号内填写变形依据。
解:原方程可变形为![]() ( )
( )
( ),得![]() ( )
( )
去括号,得![]()
( ),得![]() ( )
( )
合并同类项,得![]() (合并同类项法则)
(合并同类项法则)
( ),得![]() ( )
( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小刚从点 ![]() 出发,沿着坡度为
出发,沿着坡度为 ![]() 的斜坡向上走了650米到达点
的斜坡向上走了650米到达点 ![]() ,且
,且 ![]() .
.
(1)则他上升的高度是 米 ;
(2)然后又沿着坡度为 ![]() 的斜坡向上走了1000米达到点
的斜坡向上走了1000米达到点 ![]() .问小刚从
.问小刚从 ![]() 点到
点到 ![]() 点上升的高度
点上升的高度 ![]() 是多少米(结果保留根号)?
是多少米(结果保留根号)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为深化义务教育课程改革,满足学生的个性化学习需求,某校就“学生对知识拓展、体育特长、艺术特长和时间活动四类选课意向”进行了抽样调查(每人选报一类),绘制了如图所示的两幅统计图(不完整),请根据图中信息,解答下列问题.


(1)求扇形统计图中的m的值,并补全条形统计图;
(2)已知该校800名学生,计划开设“实践活动类”课程,每班安排20人,问学校开设多少个“实践活动课”课程的班级比较合理.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系 ![]() 中,矩形
中,矩形 ![]() 的边
的边 ![]() 在
在 ![]() 轴上,顶点
轴上,顶点 ![]() 在抛物线
在抛物线 ![]() 上,且抛物线交
上,且抛物线交 ![]() 轴于另一点
轴于另一点 ![]() .
.
(1)则 ![]() = ,
= , ![]() =;
=;
(2)已知 ![]() 为
为 ![]() 边上一个动点(不与
边上一个动点(不与 ![]() 、
、 ![]() 重合),连结
重合),连结 ![]() 交
交 ![]() 于点
于点 ![]() ,过点
,过点 ![]() 作
作 ![]() 轴的平行线分别交抛物线、直线
轴的平行线分别交抛物线、直线 ![]() 于
于 ![]() 、
、 ![]() .
.
①求线段 ![]() 的最大值,此时
的最大值,此时 ![]() 的面积为;
的面积为;
②若以点 ![]() 为圆心,
为圆心, ![]() 为半径作⊙O,试判断直线
为半径作⊙O,试判断直线 ![]() 与⊙O的能否相切,若能请求出
与⊙O的能否相切,若能请求出 ![]() 点坐标,若不能请说明理由.
点坐标,若不能请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,EF∥AD,∠1=∠2.证明:∠DGA+∠BAC=180°.请完成说明过程.
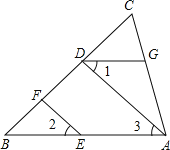
解:∵EF∥AD,(已知)
∴∠2=∠3.( )
又∵∠1=∠2(已知)
∴∠1=∠3,(等量代换)
∴AB∥ ,( )
∴∠DGA+∠BAC=180°.( )
查看答案和解析>>
科目:初中数学 来源: 题型:
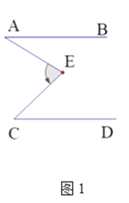
【题目】如图,AB∥CD.
(1)如图1,若∠A=35°,∠C=48°则∠E= °.
(2)如图2,若∠E=120°,∠C=110°,求∠A+∠F的度数;
(3)如图3,若∠E=110°,![]()
![]() ,若GD∥FC,请直接写出∠AGF与∠GDC的数量关系: .
,若GD∥FC,请直接写出∠AGF与∠GDC的数量关系: .


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com