
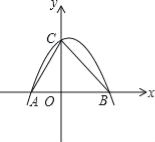
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)经过A(﹣3,0)、B(5,0)、C(0,5)三点,O为坐标原点
(1)求此抛物线的解析式;
(2)若把抛物线y=ax2+bx+c(a≠0)向下平移![]() 个单位长度,再向右平移n(n>0)个单位长度得到新抛物线,若新抛物线的顶点M在△ABC内,求n的取值范围;
个单位长度,再向右平移n(n>0)个单位长度得到新抛物线,若新抛物线的顶点M在△ABC内,求n的取值范围;
(3)设点P在y轴上,且满足∠OPA+∠OCA=∠CBA,求CP的长.
【答案】(1)y=﹣![]() x2+
x2+![]() x+5;(2)0<n<3;(3)PC的长为7或17.
x+5;(2)0<n<3;(3)PC的长为7或17.
【解析】
试题分析:(1)根据A、B、C三点的坐标,利用待定系数法可求得抛物线的解析式即可;(2)可先求得抛物线的顶点坐标,再利用坐标平移,可得平移后的坐标为(1+n,1),再由B、C两点的坐标可求得直线BC的解析式,可求得y=1时,对应的x的值,从而可求得n的取值范围;(3)当点P在y轴负半轴上和在y轴正半轴上两种情况,根据这两种情况分别求得PC的长即可.
试题解析:(1)把A、B、C三点的坐标代入函数解析式可得 ,
,
解得![]() ,
,
∴抛物线解析式为y=﹣![]() x2+
x2+![]() x+5;
x+5;
(2)∵y=﹣![]() x2+
x2+![]() x+5,
x+5,
∴抛物线顶点坐标为(1,![]() ),
),
∴当抛物线y=ax2+bx+c(a≠0)向下平移![]() 个单位长度,再向右平移n(n>0)个单位长度后,得到的新抛物线的顶点M坐标为(1+n,1),
个单位长度,再向右平移n(n>0)个单位长度后,得到的新抛物线的顶点M坐标为(1+n,1),
设直线BC解析式为y=kx+m,把B、C两点坐标代入可得![]() ,解得
,解得![]() ,
,
∴直线BC的解析式为y=﹣x+5,
令y=1,代入可得1=﹣x+5,解得x=4,
∵新抛物线的顶点M在△ABC内,
∴1+n<4,且n>0,解得0<n<3,
即n的取值范围为0<n<3;
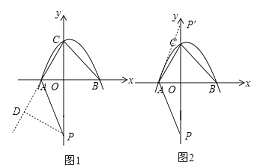
(3)当点P在y轴负半轴上时,如图1,过P作PD⊥AC,交AC的延长线于点D,
由题意可知OB=OC=5,
∴∠CBA=45°,
∴∠PAD=∠OPA+∠OCA=∠CBA=45°,
∴AD=PD,
在Rt△OAC中,OA=3,OC=5,可求得AC=![]() ,
,
设PD=AD=m,则CD=AC+AD=![]() +m,
+m,
∵∠ACO=∠PCD,∠COA=∠PDC,
∴△COA∽△CDP,
∴![]() ,即
,即![]() ,
,
解得m=![]() ,PC=17;
,PC=17;
可求得PO=PC﹣OC=17﹣5=12,
如图2,在y轴正半轴上截取OP′=OP=12,连接AP′,
则∠OP′A=∠OPA,
∴∠OP′A+∠OCA=∠OPA+∠OCA=∠CBA,
∴P′也满足题目条件,此时P′C=OP′﹣OC=12﹣5=7,
综上可知PC的长为7或17.


科目:初中数学 来源: 题型:
【题目】方格纸上有A,B两点,若以B点为原点建立平面直角坐标系,则A点坐标为(-4,3),若以A点为原点建立平面直角坐标系,则B点坐标为( )
A. (-4,-3) B. (-4,3) C. (4,-3) D. (4,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了首届“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
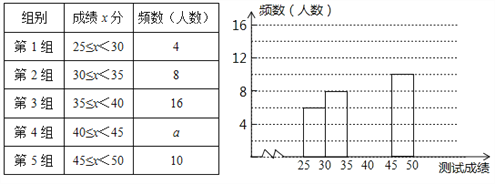
请结合图表完成下列各题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,则本次测试的优秀率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知三角形的三个顶点坐标分别是(-1,4)、(1,1)、(-4,-1),现将这三个点先向右平移2个单位长度,再向上平移3个单位长度,则平移后三个顶点的坐标是( )
A. (-2,2),(3,4),(1,7) B. (-2,2),(4,3),(1,7)
C. (2,2),(3,4),(1,7) D. (2,-2),(3,3),(1,7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育委员统计了七(1)班全体同学60秒跳绳的次数,并列出下面的频数分布表:
次数 | 60≤x<80 | 80≤x<100 | 100≤x<120 | 120≤x<140 | 140≤x<160 | 160≤x<180 | 180≤x<200 |
频数 | 2 | 4 | 21 | 14 | 7 | 3 | 1 |
给出以下结论:①全班有52个学生; ②组距是20; ③组数是7;④跳绳次数在100≤x<140范围的学生约占全班学生的67%.其中正确结论的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com