
【题目】在平面直角坐标系xOy中,定义点P(x,y)的变换点为P′(x+y,x﹣y).
(1)如图1,如果⊙O的半径为![]() ,
,
①请你判断M(2,0),N(﹣2,﹣1)两个点的变换点与⊙O的位置关系;
②若点P在直线y=x+2上,点P的变换点P′在⊙O的内,求点P横坐标的取值范围.
(2)如图2,如果⊙O的半径为1,且P的变换点P′在直线y=﹣2x+6上,求点P与⊙O上任意一点距离的最小值.

【答案】(1)①所以点N(﹣2,﹣1)的变换点在⊙O外;②点P横坐标的取值范围为﹣2<x<0;(2)点P与⊙O上任意一点距离的最小值为![]() ﹣1.
﹣1.
【解析】
试题分析:(1)①根据新定义得到点M的变换点M′的坐标为(2,2),于是根据勾股定理计算出OM′=2![]() ,则根据点与圆的位置关系的判定方法可判断点M的变换点在⊙O上;同样方法可判断点N(﹣2,﹣1)的变换点在⊙O外
,则根据点与圆的位置关系的判定方法可判断点M的变换点在⊙O上;同样方法可判断点N(﹣2,﹣1)的变换点在⊙O外
②利用一次函数图象上点的坐标特征,设P点坐标为(x,x+2),利用新定义得到P点的变换点为P′的坐标为(2x+2,﹣2),则根据勾股定理计算出OP′=![]() ,然后利用点与圆的位置关系得到
,然后利用点与圆的位置关系得到![]() <2
<2![]() ,解不等式得﹣2<x<0;
,解不等式得﹣2<x<0;
(2)设点P′的坐标为(x,﹣2x+6),P(m,n),根据新定义得到m+n=x,m﹣n=﹣2x+6,消去x得3m+n=6,则n=﹣3m+6,于是得到P点坐标为(m,﹣3m+6),则可判断点P在直线y=﹣3x+6上,设直线y=﹣3x+6与x轴相交于点A,与y轴相交于点B,过O点作OH⊥AB于H,交⊙O于C,如图2,易得A(2,0),B(0,6),利用勾股定理计算出AB=2![]() ,再利用面积法计算出OH=
,再利用面积法计算出OH=![]() ,所以CH=
,所以CH=![]() ﹣1,当点P在H点时,PC为点P与⊙O上任意一点距离的最小值.
﹣1,当点P在H点时,PC为点P与⊙O上任意一点距离的最小值.
试题解析:(1)①M(2,0)的变换点M′的坐标为(2,2),则OM′=![]() =2
=2![]() ,所以点M(2,0)的变换点在⊙O上;N(﹣2,﹣1)的变换点N′的坐标为(﹣3,﹣1),则ON′=
,所以点M(2,0)的变换点在⊙O上;N(﹣2,﹣1)的变换点N′的坐标为(﹣3,﹣1),则ON′=![]() =
=![]() >2
>2![]() ,所以点N(﹣2,﹣1)的变换点在⊙O外;
,所以点N(﹣2,﹣1)的变换点在⊙O外;
②设P点坐标为(x,x+2),则P点的变换点为P′的坐标为(2x+2,﹣2),则OP′=![]() ,∵点P′在⊙O的内,∴
,∵点P′在⊙O的内,∴![]() <2
<2![]() ,∴(2x+2)2<4,即(x+1)2<1,∴﹣1<x+1<1,解得﹣2<x<0,即点P横坐标的取值范围为﹣2<x<0;
,∴(2x+2)2<4,即(x+1)2<1,∴﹣1<x+1<1,解得﹣2<x<0,即点P横坐标的取值范围为﹣2<x<0;
(2)设点P′的坐标为(x,﹣2x+6),P(m,n),根据题意得m+n=x,m﹣n=﹣2x+6,
∴3m+n=6,即n=﹣3m+6,∴P点坐标为(m,﹣3m+6),∴点P在直线y=﹣3x+6上,
设直线y=﹣3x+6与x轴相交于点A,与y轴相交于点B,过O点作OH⊥AB于H,交⊙O于C,如图2,
则A(2,0),B(0,6),∴AB=![]() =2
=2![]() ,∵
,∵![]() OHAB=
OHAB=![]() OAOB,
OAOB,
∴OH=![]() =
=![]() ,∴CH=
,∴CH=![]() ﹣1,
﹣1,
即点P与⊙O上任意一点距离的最小值为![]() ﹣1.
﹣1.
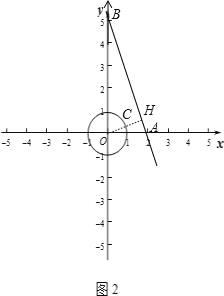


科目:初中数学 来源: 题型:
【题目】如图.从下列四个条件:①BC=B′C,②AC=A′C,③∠A′CA=∠B′CB,④AB=A′B′中,任取三个为条件,余下的一个为结论,则最多可以构成正确的结论的个数是( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD与四边形CEFG是两个正方形,边长分别为a、b.其中B、C、E在一条直线上,G在线段CD上.三角形AGE的面积为S.
(1)①当a=5,b=3时,求S的值;
②当a=7,b=3时,求S的值;
(2)从以上结果中,请你猜想S与a、b中的哪个量有关?用字母a,b表示S,并对你的猜想进行证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=90°.

①当点D在AC上时,如图(1),线段BD、CE有怎样的数量关系和位置关系?直接写出你猜想的结论;
②将图(1)中的△ADE的位置改变一下,如图(2),使∠BAD=∠CAE,其他条件不变,则线段BD,CE又有怎样的数量关系和位置关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上.将△ABC绕点A顺时针旋转90°得到△AB1C1.
(1)在网格中画出△AB1C1;
(2)计算点B旋转到B1的过程中所经过的路径长.(结果保留π)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市居民用电价格改革方案已出台,为鼓励居民节约用电,对居民生活用电实行阶梯制价格(见表):
“一户一表”用电量 | 不超过a千瓦时 | 超过a千瓦时的部分 |
单价(元/千瓦时) | 0.5 | 0.6 |
乐乐家12月份用电200千瓦时,交电费105元,则a的值为( )
A. 90 B. 100 C. 150 D. 120
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过A(﹣4,0)、B(1,0)、C(0,3)三点,直线y=mx+n经过A(﹣4,0)、C(0,3)两点.
(1)写出方程ax2+bx+c=0的解;
(2)若ax2+bx+c>mx+n,写出x的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com