
【题目】如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=90°.

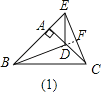
①当点D在AC上时,如图(1),线段BD、CE有怎样的数量关系和位置关系?直接写出你猜想的结论;
②将图(1)中的△ADE的位置改变一下,如图(2),使∠BAD=∠CAE,其他条件不变,则线段BD,CE又有怎样的数量关系和位置关系?请说明理由.
【答案】①BD=CE,BD⊥CE;②BD=CE,BD⊥CE,理由见解析
【解析】
试题分析:(1)BD=CE,BD⊥CE,延长BD与EC交于点F,可以证明△ACE≌△ADB,可得BD=CE,且∠BFE=90°,即可解答;
(2)BD=CE,BD⊥CE,延长BD交AC于F,交CE于H,可以证明△ACE≌△ADB,可得BD=CE,利用三角形的内角和为180°,即可得到BD⊥CE.
解:(1)BD=CE,BD⊥CE;
如图(1),延长BD与EC交于点F,
在△ACE和△ADB中,
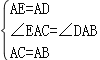 ,
,
∴△ACE≌△ADB(SAS),
∴BD=CE,∠AEC=∠ADB,
∵∠ADB+∠ABD=90°
∴∠ABD+∠AEC=90°
∴∠BFE=90°,
∴BD⊥CE.
(2)结论:BD=CE,BD⊥CE,
理由如下:∵∠BAC=∠DAE=90°
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
即∠BAD=∠CAE,
在△ABD与△ACE中,
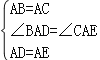
∴△ABD≌△ACE(SAS)
∴BD=CE,
如图(2),延长BD交AC于F,交CE于H.

在△ABF与△HCF中,
∵∠ABF=∠HCF,∠AFB=∠HFC
∴∠CHF=∠BAF=90°
∴BD⊥CE.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
【题目】阅读材料:
小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如3+2![]() =(1+
=(1+![]() )2.善于思考的小明进行了以下探索:
)2.善于思考的小明进行了以下探索:
设a+b![]() =(m+n
=(m+n![]() )2(其中a、b、m、n均为整数),则有a+b
)2(其中a、b、m、n均为整数),则有a+b![]() =m2+2n2+2mn
=m2+2n2+2mn![]() .
.
∴a=m2+2n2,b=2mn.这样小明就找到了一种把类似a+b![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当a、b、m、n均为正整数时,若a+b![]() =(m+n
=(m+n![]() )2,用含m、n的式子分别表示a、b,得:a= ,b= ;
)2,用含m、n的式子分别表示a、b,得:a= ,b= ;
(2)利用所探索的结论,找一组正整数a、b、m、n填空: ;
(3)若a+4![]() =(m+n
=(m+n![]() )2,且a、m、n均为正整数,求a的值?
)2,且a、m、n均为正整数,求a的值?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南宁市青秀区新开发某工程准备招标,指挥部现接到甲、乙两个工程队的投标书,从投标书中得知:乙队单独完成这项工程所需天数是甲队单独完成这项工程所需天数的2倍;该工程若由甲队先做6天,剩下的工程再由甲、乙两队合作16天可以完成.
(1)求甲、乙两队单独完成这项工程各需要多少天?
(2)已知甲队每天的施工费用为0.67万元,乙队每天的施工费用为0.33万元,该工程预算的施工费用为19万元.为缩短工期,拟安排甲、乙两队同时开工合作完成这项工程,问:该工程预算的施工费用是否够用?若不够用,需要追加预算多少万元?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列要求,解答相关问题.
(1)请补全以下求不等式﹣2x2﹣4x>0的解集的过程.
①构造函数,画出图象:根据不等式特征构造二次函数y=﹣2x2﹣4x;并在下面的坐标系中(图1)画出二次函数y=﹣2x2﹣4x的图象(只画出图象即可).
②求得界点,标示所需,当y=0时,求得方程﹣2x2﹣4x=0的解为 ;并用锯齿线标示出函数y=﹣2x2﹣4x图象中y>0的部分.
③借助图象,写出解集:由所标示图象,可得不等式﹣2x2﹣4x>0的解集为﹣2<x<0.请你利用上面求一元一次不等式解集的过程,求不等式x2﹣2x+1≥4的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】密苏里州圣路易斯拱门是座雄伟壮观的抛物线形的建筑物,是美国最高的独自挺立的纪念碑,如图.拱门的地面宽度为200米,两侧距地面高150米处各有一个观光窗,两窗的水平距离为100米,求拱门的最大高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们已经学习过了“等腰三角形的判定定理”,
(1)默写等腰三角形的判定定理(写成如果……那么……的形式):_______________________
该定理可以简写为:____________________
(2)请你结合图形,写出已知、求证,并写出证明过程.
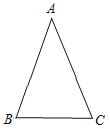
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,定义点P(x,y)的变换点为P′(x+y,x﹣y).
(1)如图1,如果⊙O的半径为![]() ,
,
①请你判断M(2,0),N(﹣2,﹣1)两个点的变换点与⊙O的位置关系;
②若点P在直线y=x+2上,点P的变换点P′在⊙O的内,求点P横坐标的取值范围.
(2)如图2,如果⊙O的半径为1,且P的变换点P′在直线y=﹣2x+6上,求点P与⊙O上任意一点距离的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
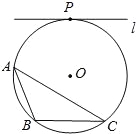
【题目】如图,⊙O为△ABC的外接圆,直线l与⊙O相切与点P,且l∥BC.
(1)请仅用无刻度的直尺,在⊙O中画出一条弦,使这条弦将△ABC分成面积相等的两部分(保留作图痕迹,不写作法);
(2)请写出证明△ABC被所作弦分成的两部分面积相等的思路.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com