
【题目】如图,四边形ABCD与四边形CEFG是两个正方形,边长分别为a、b.其中B、C、E在一条直线上,G在线段CD上.三角形AGE的面积为S.
(1)①当a=5,b=3时,求S的值;
②当a=7,b=3时,求S的值;
(2)从以上结果中,请你猜想S与a、b中的哪个量有关?用字母a,b表示S,并对你的猜想进行证明.
【答案】
(1)
解:①∵四边形ABCD与四边形CEFG是两个正方形,AB=5,EC=3,
∴DG=CD﹣CG=5﹣3=2,
∴S△AEG=S正方形ABCD+S正方形ECGF﹣S△ABE﹣S△ADG﹣S△EFG
=25+9﹣ ![]() ×8×5﹣
×8×5﹣ ![]() ×5×2﹣
×5×2﹣ ![]() ×3×3=4.5,
×3×3=4.5,
②)①∵四边形ABCD与四边形CEFG是两个正方形,AB=7,EC=3,
∴DG=CD﹣CG=7﹣3=4,
∴S△AEG=S正方形ABCD+S正方形ECGF﹣S△ABE﹣S△ADG﹣S△EFG
=49+9﹣ ![]() ×10×7﹣
×10×7﹣ ![]() ×7×4﹣
×7×4﹣ ![]() ×3×3=4.5
×3×3=4.5

(2)
解:结论S= ![]() b2.
b2.
证明:∵S△AEG=S正方形ABCD+S正方形ECGF﹣S△ABE﹣S△ADG﹣S△EFG
=a2+b2﹣ ![]() (a+b)a﹣
(a+b)a﹣ ![]() a(a﹣b)﹣
a(a﹣b)﹣ ![]() b2
b2
=a2+b2﹣ ![]() a2﹣
a2﹣ ![]() ab﹣
ab﹣ ![]() a2+
a2+ ![]() ab﹣
ab﹣ ![]() b2
b2
= ![]() b2.
b2.
∴S= ![]() b2
b2
【解析】(1)①根据S△AEG=S正方形ABCD+S正方形ECGF﹣S△ABE﹣S△ADG﹣S△EFG即可解决问题.
②方法同上.(2)结论S= ![]() b2 . 根据S△AEG=S正方形ABCD+S正方形ECGF﹣S△ABE﹣S△ADG﹣S△EFG即可证明.
b2 . 根据S△AEG=S正方形ABCD+S正方形ECGF﹣S△ABE﹣S△ADG﹣S△EFG即可证明.
【考点精析】关于本题考查的平行四边形的性质,需要了解平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】挑战自我!
下图是由一些火柴棒搭成的图案: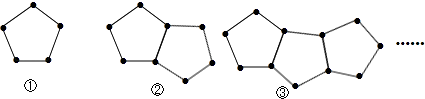
(1)摆第①个图案用几根火柴棒,
摆第②个图案用几根火柴棒,
摆第③个图案用几根火柴棒.
(2)按照这种方式摆下去,摆第n个图案用多少根火柴棒?
(3)计算一下摆121根火柴棒时,是第几个图案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,AD,BC是⊙O的两条互相垂直的直径,点P从点O出发沿图中某一个扇形顺时针匀速运动,设∠APB=y(单位:度),如果y与点P运动的时间x(单位:秒)的函数关系的图象大致如图2所示,那么点P的运动路线可能为( )

A.O→B→A→O B.O→A→C→O C.O→C→D→O D.O→B→D→O
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南宁市青秀区新开发某工程准备招标,指挥部现接到甲、乙两个工程队的投标书,从投标书中得知:乙队单独完成这项工程所需天数是甲队单独完成这项工程所需天数的2倍;该工程若由甲队先做6天,剩下的工程再由甲、乙两队合作16天可以完成.
(1)求甲、乙两队单独完成这项工程各需要多少天?
(2)已知甲队每天的施工费用为0.67万元,乙队每天的施工费用为0.33万元,该工程预算的施工费用为19万元.为缩短工期,拟安排甲、乙两队同时开工合作完成这项工程,问:该工程预算的施工费用是否够用?若不够用,需要追加预算多少万元?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)请你任意写出五个正的真分数:_____、_____、_____、_____、_____.请给每个分数的分子和分母同加上一个正数得到五个新分数:_____、_____、_____、_____、_____.
(2)比较原来每个分数与对应新分数的大小,可以得出下面的结论:一个真分数是![]() (a、b均为正数,a<b)给其分子、分母同加上一个正数m,得
(a、b均为正数,a<b)给其分子、分母同加上一个正数m,得![]() ,则两个分数的大小关系是:
,则两个分数的大小关系是: ![]() _____
_____![]() .
.
(3)请你用文字叙述(2)中结论的含义:_______________________________________.
(4)你能用图形的面积说明这个结论吗?
(5)解决问题:如图所示,有一个长宽不等的长方形绿地,现给绿地四周铺一条宽相等的小路,原来的绿地与现在铺过小路后的绿地的长与宽的比值是否相等?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列要求,解答相关问题.
(1)请补全以下求不等式﹣2x2﹣4x>0的解集的过程.
①构造函数,画出图象:根据不等式特征构造二次函数y=﹣2x2﹣4x;并在下面的坐标系中(图1)画出二次函数y=﹣2x2﹣4x的图象(只画出图象即可).
②求得界点,标示所需,当y=0时,求得方程﹣2x2﹣4x=0的解为 ;并用锯齿线标示出函数y=﹣2x2﹣4x图象中y>0的部分.
③借助图象,写出解集:由所标示图象,可得不等式﹣2x2﹣4x>0的解集为﹣2<x<0.请你利用上面求一元一次不等式解集的过程,求不等式x2﹣2x+1≥4的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】密苏里州圣路易斯拱门是座雄伟壮观的抛物线形的建筑物,是美国最高的独自挺立的纪念碑,如图.拱门的地面宽度为200米,两侧距地面高150米处各有一个观光窗,两窗的水平距离为100米,求拱门的最大高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,定义点P(x,y)的变换点为P′(x+y,x﹣y).
(1)如图1,如果⊙O的半径为![]() ,
,
①请你判断M(2,0),N(﹣2,﹣1)两个点的变换点与⊙O的位置关系;
②若点P在直线y=x+2上,点P的变换点P′在⊙O的内,求点P横坐标的取值范围.
(2)如图2,如果⊙O的半径为1,且P的变换点P′在直线y=﹣2x+6上,求点P与⊙O上任意一点距离的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(3分)有13位同学参加学校组织的才艺表演比赛.已知他们所得的分数互不相同,共设7个获奖名额.某同学知道自己的比赛分数后,要判断自己能否获奖,在下列13名同学成绩的统计量中只需知道一个量,它是( )
A. 众数 B. 方差 C. 中位数 D. 平均数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com