
【题目】如图,直线![]() 与反比例函数
与反比例函数![]() 的图象交于点
的图象交于点![]() 与
与![]() 轴交于点
轴交于点![]() 平行于
平行于![]() 轴的直线
轴的直线![]() 交反比例函数的图象于点
交反比例函数的图象于点![]() 交线段
交线段![]() 于点
于点![]() 连接
连接![]() .
.
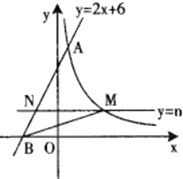
(1)求![]() 的值和反比例函数的表达式;
的值和反比例函数的表达式;
(2)当点![]() 是线段
是线段![]() 的中点时,求点
的中点时,求点![]() 的坐标;
的坐标;
(3)直线![]() 沿
沿![]() 轴方向平移,当
轴方向平移,当![]() 为何值时,
为何值时,![]() 的面积最大?
的面积最大?
科目:初中数学 来源: 题型:
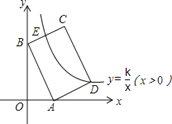
【题目】在平面直角坐标系xOy中,函数![]() (x>0)的图象与直线l1:
(x>0)的图象与直线l1:![]() 交于点A,与直线l2:x=k交于点B.直线l1与l2交于点C.
交于点A,与直线l2:x=k交于点B.直线l1与l2交于点C.

(1) 当点A的横坐标为1时,则此时k的值为 _______;
(2) 横、纵坐标都是整数的点叫做整点. 记函数![]() (x>0) 的图像在点A、B之间的部分与线段AC,BC围成的区域(不含边界)为W.
(x>0) 的图像在点A、B之间的部分与线段AC,BC围成的区域(不含边界)为W.
①当k=3时,结合函数图像,则区域W内的整点个数是_________;
②若区域W内恰有1个整点,结合函数图象,直接写出k的取值范围:___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知梯形ABCD中,AD∥BC,AB=AC,E是边BC上的点,且∠AED=∠CAD,DE交AC于点F.
(1)求证:△ABE∽△DAF;
(2)当ACFC=AEEC时,求证:AD=BE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形ABCD的边AB:BC=3:2,点A(3,0),B(0,6)分别在x轴,y轴上,反比例函数y=![]() (x>0)的图象经过点D,且与边BC交于点E,则点E的坐标为__.
(x>0)的图象经过点D,且与边BC交于点E,则点E的坐标为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形 ABCD 中, P 为 AB 的中点,![]() 的延长线于点 E ,连接 AE 、 BE ,
的延长线于点 E ,连接 AE 、 BE ,![]() 交 DP 于点 F ,连接 BF 、FC ,下列结论:①
交 DP 于点 F ,连接 BF 、FC ,下列结论:① ![]() ;② FB AB ;③
;② FB AB ;③ ![]() ;④ FC EF . 其中正确的是( )
;④ FC EF . 其中正确的是( )
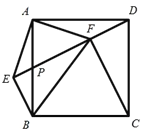
A.①②④B.①③④C.①②③D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段OA=2,OP=1,将线段OP绕点O任意旋转时,线段AP的长度也随之改变,则下列结论:
①AP的最小值是1,最大值是4;
②当AP=2时,△APO是等腰三角形;
③当AP=1时,△APO是等腰三角形;
④当AP=![]() 时,△APO是直角三角形;
时,△APO是直角三角形;
⑤当AP=![]() 时,△APO是直角三角形.
时,△APO是直角三角形.
其中正确的是( )
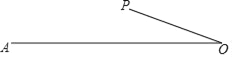
A. ①④⑤ B. ②③⑤ C. ②④⑤ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为初三学生定制校服,对部分学生的服装型号做了调查,结果如下:
型号 | 140 | 150 | 160 | 170 | 180 |
男生 | 11 | 18 | 9 | 7 | 5 |
女生 | 9 | 12 | 18 | 7 | 4 |
下列说法正确的是( )
A.男生服装型号的众数大于女生服装型号的众数
B.男生服装型号的中位数等于女生服装型号的中位数
C.男生服装型号的众数小于女生服装型号的众数
D.男生服装型号的中位数大于女生服装型号的中位数
查看答案和解析>>
科目:初中数学 来源: 题型:
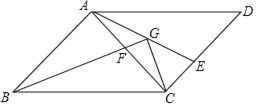
【题目】在平行四边形ABCD中,∠ABC=45°,AB=AC,点E,F分别CD、AC边上的点,且AF=CE,BF的延长线交AE于点G.
(1)若DE=2![]() ,AD=8,求AE.
,AD=8,求AE.
(2)若G是AE的中点,连接CG,求证:![]() AE+CG=BG.
AE+CG=BG.
查看答案和解析>>
科目:初中数学 来源: 题型:
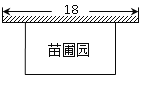
【题目】某课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米.
(1)若苗圃园的面积为72平方米,求x;
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由;
(3)当这个苗圃园的面积不小于100平方米时,直接写出x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com