
���� ��1����ֱ�߽���ʽ���ֱ���x��yΪ0���y��x��ֵ��ȷ����A��B���꣬��C��x��y����x��0��y��0�������������BC2=AC2��BC2+AC2=AB2���г�����x��y�ķ����飬���������Ľ�õ�x��y��ֵ������ȷ����C�����ꣻ���ݻ��ഹֱ����ֱ��б��֮��Ϊ-1����������ֱ�߽���ʽΪy=$\frac{1}{3}$x+b����C������������b��ֵ���ɣ�
��2���������ABC�����=10����ô��ABM�����=10�����ݵ�P��x0��y0����ֱ��Ax+By+C=0��A2+B2��0���ľ���d=$\frac{|A{x}_{0}+B{y}_{0}+C|}{\sqrt{{A}^{2}+{B}^{2}}}$�Ĺ�ʽ�����M��m��1����ֱ��AB��3x+y+6=0�ľ���d����ABM��AB�ߵĸߣ��ٸ��������ʽ�ó�����m�ķ��̣��ⷽ�̼��ɣ�
��� �⣺��1������ֱ��y=-3x-6��
��x=0���õ�y=-6����y=0���õ�x=-2��
��A��-2��0����B��0��-6����
��AB2=22+62=40��
��C��x��y����x��0��y��0����
��������ã�BC2=AC2��BC2+AC2=AB2��
��$\left\{\begin{array}{l}{{x}^{2}+��y+6��^{2}=��x+2��^{2}+{y}^{2}}\\{{x}^{2}+��y+6��^{2}+��x+2��^{2}+{y}^{2}=40}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{{x}_{1}=-4}\\{{y}_{1}=-4}\end{array}\right.$��$\left\{\begin{array}{l}{{x}_{2}=2}\\{{y}_{2}=-2}\end{array}\right.$������������ȥ����
��C��-4��-4����
�����C����ֱ��AB��ֱ��ֱ�߷�����y=$\frac{1}{3}$x+b��
��C��������룬��-$\frac{4}{3}$+b=-4��
���b=-$\frac{8}{3}$��
�����C����ֱ��AB��ֱ��ֱ�߷�����y=$\frac{1}{3}$x-$\frac{8}{3}$��
��2���ߡ�ABC�����=$\frac{1}{2}$AC•BC=$\frac{1}{2}$AC2=$\frac{1}{4}$AB2=10��
���ABM�����=10��
�ߵ�M��m��1����ֱ��AB��3x+y+6=0�ľ���d=$\frac{|A{x}_{0}+B{y}_{0}+C|}{\sqrt{{A}^{2}+{B}^{2}}}$=$\frac{|3m+1+6|}{\sqrt{{3}^{2}+{1}^{2}}}$=$\frac{|3m+7|}{\sqrt{10}}$��AB=$\sqrt{40}$=2$\sqrt{10}$��
���ABM�����=$\frac{1}{2}$��2$\sqrt{10}$��$\frac{|3m+7|}{\sqrt{10}}$=|3m+7|��
��|3m+7|=10��
���m=1��-$\frac{17}{3}$��
������m��ֵΪ1��-$\frac{17}{3}$��
���� ���⿼���˴���ϵ������һ�κ�������ʽ��һ�κ�����������Ľ��㣬�����ľ��빫ʽ������ֱ�������ε����ʣ������ε��������������һ�κ����������ǽⱾ��Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
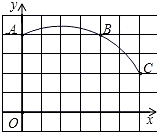 ��ͼ��ֱ������ϵ��һ��Բ�����������A��B��C�����У�B������Ϊ��4��4����C������Ϊ��6��2����D������Ϊ��7��0������֤��ֱ��CD��Բ�����ߣ�
��ͼ��ֱ������ϵ��һ��Բ�����������A��B��C�����У�B������Ϊ��4��4����C������Ϊ��6��2����D������Ϊ��7��0������֤��ֱ��CD��Բ�����ߣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ֱ��l1����A��8��0����B��0��-5����ֱ��l2����C��0��-1����l1��l2�ཻ�ڵ�D���ҡ�DCB���������8��
��ͼ��ֱ��l1����A��8��0����B��0��-5����ֱ��l2����C��0��-1����l1��l2�ཻ�ڵ�D���ҡ�DCB���������8���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪��ABC�DZ߳�Ϊ12cm�ĵȱ������Σ�����P��Qͬʱ��AB����������ֱ���AB��BC�����˶������е�P�˶����ٶ���2cm/s����Q�˶����ٶ���4cm/s������Q�����Cʱ��P��Q���㶼ֹͣ�˶������˶�ʱ��Ϊt��s��������������⣺
��ͼ����֪��ABC�DZ߳�Ϊ12cm�ĵȱ������Σ�����P��Qͬʱ��AB����������ֱ���AB��BC�����˶������е�P�˶����ٶ���2cm/s����Q�˶����ٶ���4cm/s������Q�����Cʱ��P��Q���㶼ֹͣ�˶������˶�ʱ��Ϊt��s��������������⣺�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
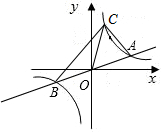 ��ͼ������������y=$\frac{3}{x}$��ͼ����ֱ��y=ax��a��0������A��B���㣬��A�ĺ�����Ϊ3��
��ͼ������������y=$\frac{3}{x}$��ͼ����ֱ��y=ax��a��0������A��B���㣬��A�ĺ�����Ϊ3���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com