
ЁОЬтФПЁПШчЭМ1ЃЌдкЬнаЮABCDжаЃЌABЁЮCDЃЌЁЯB=90ЁуЃЌAB=2ЃЌCD=1ЃЌBC=mЃЌPЮЊЯпЖЮBCЩЯЕФвЛЖЏЕуЃЌЧвКЭBЁЂCВЛжиКЯЃЌСЌНгPAЃЌЙ§PзїPEЁЭPAНЛCDЫљдкжБЯпгкEЃЎЩшBP=xЃЌCE=yЃЎ

ЃЈ1ЃЉЧѓyгыxЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉШєЕуPдкЯпЖЮBCЩЯдЫЖЏЪБЃЌЕуEзмдкЯпЖЮCDЩЯЃЌЧѓmЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌШєm=4ЃЌНЋЁїPECбиPEЗелжСЁїPEGЮЛжУЃЌЁЯBAG=90ЁуЃЌЧѓBPГЄЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]()
ЃЈ2ЃЉ0ЃМ![]()
ЃЈ3ЃЉBPЕФГЄЮЊ![]() Лђ2
Лђ2
ЁОНтЮіЁП
ЗжЮіЃКЃЈ1ЃЉжЄУїЁїABPЁзЁїPCEЃЌРћгУБШР§ЯпЖЮЙиЯЕЧѓГіyгыxЕФКЏЪ§ЙиЯЕЪНЁЃ
ЃЈ2ЃЉИљОнЃЈ1ЃЉжаЧѓГіЕФyгыxЕФЙиЯЕЪНЃЌРћгУЖўДЮКЏЪ§аджЪЃЌЧѓГіЦфзюДѓжЕЃЌСаВЛЕШЪНШЗЖЈmЕФШЁжЕЗЖЮЇЁЃ
ЃЈ3ЃЉИљОнЗелЕФаджЪМАвбжЊЬѕМўЃЌЙЙдьжБНЧШ§НЧаЮЃЌРћгУЙДЙЩЖЈРэЧѓГіBPЕФГЄЖШЁЃ
НтЃКЃЈ1ЃЉЁпЁЯAPB+ЁЯCPE=90ЁуЃЌЁЯCEP+ЁЯCPE=90ЁуЃЌЁрЁЯAPB=ЁЯCEPЁЃ
гжЁпЁЯB=ЁЯC=90ЁуЃЌЁрЁїABPЁзЁїPCEЁЃ
Ёр![]() ЃЌМД
ЃЌМД![]() ЁЃ
ЁЃ
ЁрyгыxЕФКЏЪ§ЙиЯЕЪНЮЊ![]() ЁЃ
ЁЃ
ЃЈ2ЃЉЁп![]() ЃЌ
ЃЌ
ЁрЕБx=![]() ЪБЃЌyШЁЕУзюДѓжЕЃЌзюДѓжЕЮЊ
ЪБЃЌyШЁЕУзюДѓжЕЃЌзюДѓжЕЮЊ![]() ЁЃ
ЁЃ
ЁпЕуPдкЯпЖЮBCЩЯдЫЖЏЪБЃЌЕуEзмдкЯпЖЮCDЩЯЃЌ
Ёр![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЁЃ
ЁЃ
ЁпmЃО0ЃЌЁрmЕФШЁжЕЗЖЮЇЮЊЃК0ЃМ![]() ЁЃ
ЁЃ
ЃЈ3ЃЉгЩелЕўПЩжЊЃЌPG=PCЃЌEG=ECЃЌЁЯGPE=ЁЯCPEЃЌ
гжЁпЁЯGPE+ЁЯAPG=90ЁуЃЌЁЯCPE+ЁЯAPB=90ЁуЃЌ
ЁрЁЯAPG=ЁЯAPBЁЃ
ЁпЁЯBAG=90ЁуЃЌЁрAGЁЮBCЁЃЁрЁЯGAP=ЁЯAPBЁЃ
ЁрЁЯGAP=ЁЯAPGЁЃЁрAG=PG=PCЁЃ
ШчЭМЃЌЗжБ№бгГЄCEЁЂAGЃЌНЛгкЕуHЃЌ
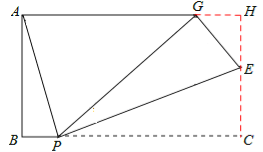
дђвзжЊABCHЮЊОиаЮЃЌHE=CHЉCE=2ЉyЃЌ![]() ЃЌ
ЃЌ
дкRtЁїGHEжаЃЌгЩЙДЙЩЖЈРэЕУЃКGH2+HE2=GH2ЃЌ
МДЃКx2+ЃЈ2ЉyЃЉ2=y2ЃЌЛЏМђЕУЃКx2Љ4y+4=0 Ђй
гЩЃЈ1ЃЉПЩжЊ![]() ЃЌетРяm=4ЃЌЁр
ЃЌетРяm=4ЃЌЁр![]() ЁЃ
ЁЃ
ДњШыЂйЪНећРэЕУЃКx2Љ8x+4=0ЃЌНтЕУЃКx=![]() Лђx=2ЁЃ
Лђx=2ЁЃ
ЁрBPЕФГЄЮЊ![]() Лђ2ЁЃ
Лђ2ЁЃ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃЌШчЭМЃЌдкЦНааЫФБпаЮABCDжаЃЌBFЦНЗж![]() НЛADгкЕуFЃЌAE
НЛADгкЕуFЃЌAE![]() BFгкЕуOЃЌНЛBCгкЕуEЃЌСЌНгEFЃЎ
BFгкЕуOЃЌНЛBCгкЕуEЃЌСЌНгEFЃЎ
ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮABEFЪЧСтаЮЃЛ
ЃЈ2ЃЉШєAE=6ЃЌBF=8ЃЌCE=3ЃЌЧѓЫФБпаЮABCDЕФУцЛ§ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() жсЕФЦНааЯпЃЌНЛ
жсЕФЦНааЯпЃЌНЛ![]() жсгкЕу
жсгкЕу![]() ЃЌЧвШ§НЧаЮ
ЃЌЧвШ§НЧаЮ![]() ЕФУцЛ§ЪЧ
ЕФУцЛ§ЪЧ![]() .
.
ЃЈ![]() ЃЉЧѓЕу
ЃЉЧѓЕу![]() ЃЌ
ЃЌ![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ![]() ЃЉЕу
ЃЉЕу![]() ЃЌ
ЃЌ![]() ЗжБ№ЮЊЯпЖЮ
ЗжБ№ЮЊЯпЖЮ![]() ЃЌ
ЃЌ![]() ЩЯЕФСНИіЖЏЕуЃЌЕу
ЩЯЕФСНИіЖЏЕуЃЌЕу![]() ДгЕу
ДгЕу![]() Яђзѓвд
Яђзѓвд![]() ИіЕЅЮЛГЄЖШ/УыдЫЖЏЃЌЭЌЪБЕу
ИіЕЅЮЛГЄЖШ/УыдЫЖЏЃЌЭЌЪБЕу![]() ДгЕу
ДгЕу![]() ЯђЕу
ЯђЕу![]() вд
вд![]() ИіЕЅЮЛГЄЖШ/УыдЫЖЏЃЌШчЭМЫљЪОЃЌЩшдЫЖЏЪБМфЮЊ
ИіЕЅЮЛГЄЖШ/УыдЫЖЏЃЌШчЭМЫљЪОЃЌЩшдЫЖЏЪБМфЮЊ![]() Уы
Уы![]() .
.
ЂйЕБ![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЂкЪЧЗёДцдквЛЖЮЪБМфЃЌЪЙЕУ![]() ЃПШєДцдкЃЌЧѓГі
ЃПШєДцдкЃЌЧѓГі![]() ЕФШЁжЕЗЖЮЇЃЛШєВЛДцдкЃЌЫЕУїРэгЩ.
ЕФШЁжЕЗЖЮЇЃЛШєВЛДцдкЃЌЫЕУїРэгЩ.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГВЭЬќжаЃЌвЛеХзРзгПЩзј6ШЫЃЌгаШчЭМЫљЪОЕФСНжжАкЗХЗНЪНЃК

ЃЈ1ЃЉЕБгаnеХзРзгЪБЃЌСНжжАкЗХЗНЪНИїФмзјЖрЩйШЫЃП
ЃЈ2ЃЉвЛЬьжаЮчВЭЬќвЊНгД§98ЮЛЙЫПЭЙВЭЌОЭВЭЃЌЕЋВЭЬќжЛга25еХетбљЕФВЭзР.ШєФуЪЧетИіВЭЬќЕФОРэЃЌФуДђЫубЁдёФФжжЗНЪНРДАкЗХВЭзРЃПЮЊЪВУДЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ![]() ЪЧЕШБпШ§НЧаЮЃЌ
ЪЧЕШБпШ§НЧаЮЃЌ![]() ЩЯгаЕуDЃЌЗжБ№вд
ЩЯгаЕуDЃЌЗжБ№вд![]() ЮЊБпзїЕШБп
ЮЊБпзїЕШБп![]() КЭЕШбќ
КЭЕШбќ![]() ЃЌБп
ЃЌБп![]() ЁЂ
ЁЂ![]() НЛгкЕуHЃЌЕуFдк
НЛгкЕуHЃЌЕуFдк![]() бгГЄЯпЩЯЧв
бгГЄЯпЩЯЧв![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЎЧѓжЄЃК
ЃЎЧѓжЄЃК

ЃЈ1ЃЉ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉ![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌеХШ§ДђЫудкдКТфжжЩЯЪпВЫЃЎвбжЊдКТфЮЊЖЋЮїГЄЮЊ32УзЃЌФЯББПэЮЊ20УзЕФГЄЗНаЮЃЌЮЊСЫаазпЗНБуЃЌвЊаожўЭЌбљПэЖШЕФШ§ЬѕаЁТЗЃЌЖЋЮїСНЬѕЃЌФЯББвЛЬѕЃЌгрЯТЕФВПЗжжжЩЯИїРрЪпВЫЃЎШєУПЬѕаЁТЗЕФПэОљЮЊ1УзЃЎ
ЃЈ1ЃЉЧѓЪпВЫЕФжжжВУцЛ§ЃЛ
ЃЈ2ЃЉШєУПЦНЗНУзЕФУПМОЪпВЫЕФжЕЮЊ3дЊЃЌГЩБОЮЊ1дЊЃЌетИідКТфУПМОЕФВњжЕЪЧЖрЩйЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕуAЃЌBЃЌCдкЁбOЩЯЃЌШєЁЯBACЃН45ЁуЃЌOBЃН2ЃЌдђЭМжавѕгАВПЗжЕФУцЛ§ЮЊ( )

A. ІаЃ4 B. ![]() ІаЃ1 C. ІаЃ2 D.
ІаЃ1 C. ІаЃ2 D. ![]() Ѓ2
Ѓ2
ЁОД№АИЁПC
ЁОНтЮіЁПЪдЬтНтЮіЃКЁпЁЯBAC=45ЁуЃЌ
ЁрЁЯBOC=90ЁуЃЌ
ЁрЁїOBCЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁпOB=2ЃЌ
ЁрЁїOBCЕФBCБпЩЯЕФИпЮЊЃК![]() OB=
OB=![]() ЃЌ
ЃЌ
ЁрBC=2![]()
ЁрSвѕгА=SЩШаЮOBCЉSЁїOBC=![]() .
.
ЙЪбЁCЃЎ
ЁОЬтаЭЁПЕЅбЁЬт
ЁОНсЪјЁП
10
ЁОЬтФПЁПЯФМОЕФвЛЬьЃЌЩэИпЮЊ1.6mЕФаЁСсЯыВтСПвЛЯТЮнЧАДѓЪїЕФИпЖШЃЌЫ§бизХЪїгАBAгЩBЕНAзпШЅЃЌЕБзпЕНCЕуЪБЃЌЫ§ЕФгАзгЖЅЖЫе§КУгыЪїЕФгАзгЖЅЖЫжиКЯЃЌВтЕУBC=3.2mЃЌCA=0.8mЃЌгкЪЧЕУГіЪїЕФИпЖШЮЊ(ЁЁЁЁ)

AЃЎ8m BЃЎ6.4m CЃЎ4.8m DЃЎ10m
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌMЃЌNЮЊЩНСНВрЕФСНИіДхзЏЃЌЮЊСЫСНДхНЛЭЈЗНБуЃЌИљОнЙњМвЕФЛнУёеўВпЃЌеўИЎОіЖЈДђвЛжБЯпКЖДЃЌЙЄГЬШЫдБЮЊМЦЫуЙЄГЬСПЃЌБиаыВтСПMЁЂNСНЕужЎМфЕФжБЯпОрРыЃЎбЁдёВтСПЕуAЁЂBЁЂCЃЌЕуBЁЂCЗжБ№дкAMЁЂANЩЯЃЌЯжВтЕУAMЃН1ЧЇУзЃЌANЃН1.8ЧЇУзЃЌABЃН54УзЃЌBCЃН45УзЃЌACЃН30УзЃЌЧѓMЁЂNСНЕужЎМфЕФжБЯпОрРыЃЎ

ЁОД№АИЁПMЁЂNСНЕужЎМфЕФжБЯпОрРыЮЊ1500УзЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЯШИљОнЯрЫЦШ§НЧаЮЕФХаЖЈЕУГіЁїABCЁзЁїAMNЃЌдйРћгУЯрЫЦШ§НЧаЮЕФаджЪНтД№МДПЩЃЎ
ЪдЬтНтЮіЃКдкЁїABCгыЁїAMNжаЃЌ ![]() ЃЌ
ЃЌ ![]() =
=![]() ЃЌЁр
ЃЌЁр![]() ЃЌгжЁпЁЯA=ЁЯAЃЌ
ЃЌгжЁпЁЯA=ЁЯAЃЌ
ЁрЁїABCЁзЁїAMNЃЌЁр![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ
НтЕУЃКMN=1500УзЃЌ
Д№ЃКMЁЂNСНЕужЎМфЕФжБЯпОрРыЪЧ1500УзЃЛ
ПМЕуЃКЯрЫЦШ§НЧаЮЕФгІгУЃЎ
ЁОЬтаЭЁПНтД№Ьт
ЁОНсЪјЁП
23
ЁОЬтФПЁПШчЭМЃЌдкЁїADCжаЃЌЕуBЪЧБпDCЩЯЕФвЛЕуЃЌЁЯDAB=ЁЯCЃЌ ![]() ЃЎШєЁїADCЕФУцЛ§ЮЊ18cmЃЌЧѓЁїABCЕФУцЛ§ЃЎ
ЃЎШєЁїADCЕФУцЛ§ЮЊ18cmЃЌЧѓЁїABCЕФУцЛ§ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкбЇаЃзщжЏЕФЩчЛсЪЕМљЛюЖЏжаЃЌЕквЛаЁзщИКд№ЕїВщШЋаЃ10000УћЭЌбЇУПЬьЭъГЩМвЭЅзївЕЪБМфЧщПіЃЌЫћУЧЫцЛњГщШЁСЫвЛВПЗжЭЌбЇНјааЕїВщЃЌОЎЛцжЦСЫЫљГщШЁбљБОЕФЦЕЪ§ЗжВМБэКЭЖюЪ§ЗжВМжБЗНЭМ(ШчЭМ).
ЪБМфxЃЈаЁЪБЃЉ | ЦЕЪ§ | АйЗжБШ |
0.5Ёмx<1 | 4 | 8ЃЅ |
1Ёмx<1.5 | 5 | 10ЃЅ |
1.5Ёмx<2 | a | 40ЃЅ |
2Ёмx<2.5 | 15 | 30ЃЅ |
2.5Ёмx<3 | 4 | 8ЃЅ |
xЁн3 | 2 | b |
ЦЕЪ§ЗжВМБэ

ЧыИљОнЭМжааХЯЂНтД№ЯТСаЮЪЬтЃК
(1)ИУаЁзщвЛЙВГщВщСЫ___________ШЫЃЛ
(2)ЦЕЪ§ЗжВМБэжаЕФa=___________ЃЌb=____________ЃЛ
(3)НЋЦЕЪ§ЗжВМжБЗНЭМВЙГфЭъећ(жБНгЛЭМЃЌВЛаДМЦЫуЙ§ГЬ)ЃЛ
(4)ЁЖСЩФўЪЁТфЪЕНЬг§ВПЕШОХВПУХЙигкжааЁбЇЩњМѕИКДыЪЉЪЕЪЉЗНАИЁЗЙцЖЈЃЌГѕжаЩњУПЬьЪщУцМвЭЅзївЕЪБМфВЛГЌЙ§1.5аЁЪБЃЌИљОнБэжаЪ§ОнЃЌЧыФуЬсГіКЯРэЛЏНЈвщ.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com