
分析 由单独由人工清理共需要40小时,可知人工清理的效率为$\frac{1}{40}$,则机械清理的效率是$\frac{1}{40}$×8,设机械清理还需要x小时才能全部清理完,等量关系为:人工清理4小时完成的工作量+机械清理x小时完成的工作量=1,依此列出方程,解方程即可.
解答 解:设机械清理还需要x小时才能全部清理完,根据题意得
$\frac{1}{40}$×4+$\frac{1}{40}$×8x=1,
解得x=$\frac{9}{2}$.
答:机械清理还需要$\frac{9}{2}$小时才能全部清理完.
点评 本题考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案科目:初中数学 来源: 题型:选择题
 如图,已知a∥b,将一块三角尺放在这两条直线之间,使直角顶点在直线a上,较小的锐角的顶点在直线b上.若∠1=25°,则∠2的度数为( )
如图,已知a∥b,将一块三角尺放在这两条直线之间,使直角顶点在直线a上,较小的锐角的顶点在直线b上.若∠1=25°,则∠2的度数为( )| A. | 25° | B. | 35° | C. | 55° | D. | 65° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{400}{x-20}$=$\frac{320}{x}$ | B. | $\frac{400}{x+20}$=$\frac{320}{x}$ | C. | $\frac{400}{x}$+20=$\frac{320}{x}$ | D. | $\frac{400}{x}$=$\frac{320}{x+20}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
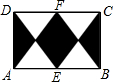 如图,一个矩形区域ABCD,点E、F分别是AB、DC的中点,则一只蝴蝶落在阴影部分的概率是( )
如图,一个矩形区域ABCD,点E、F分别是AB、DC的中点,则一只蝴蝶落在阴影部分的概率是( )| A. | $\frac{1}{4}$ | B. | $\frac{17}{38}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
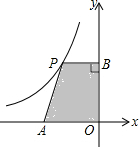 如图,平面直角坐标系中,点A是x轴负半轴上一个定点,点P是函数$y=-\frac{4}{x}$(x<0)上一个动点,PB⊥y轴于点B,当点P的横坐标逐渐增大时,四边形OAPB的面积将会( )
如图,平面直角坐标系中,点A是x轴负半轴上一个定点,点P是函数$y=-\frac{4}{x}$(x<0)上一个动点,PB⊥y轴于点B,当点P的横坐标逐渐增大时,四边形OAPB的面积将会( )| A. | 逐渐增大 | B. | 先减后增 | C. | 逐渐减小 | D. | 先增后减 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
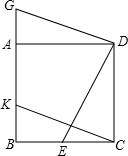 如图,四边形ABCD是正方形,点E、K分别在BC、AB上,且CE=BK,并将△DCE绕点D顺时针旋转90°得到△DAG.
如图,四边形ABCD是正方形,点E、K分别在BC、AB上,且CE=BK,并将△DCE绕点D顺时针旋转90°得到△DAG.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com