
【题目】为方便市民低碳生活绿色出行,市政府计划改造如图所示的人行天桥:天桥的高是10米,原坡面倾斜角∠CAB=45°.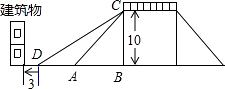
(1)若新坡面倾斜角∠CDB=28°,则新坡面的长CD长是多少?(精确到0.1米)
(2)若新坡角顶点D前留3米的人行道,要使离原坡角顶点A处10米的建筑物不拆除,新坡面的倾斜角∠CDB度数的最小值是多少?(精确到1°)
【答案】
(1)解:在Rt△BCD中,
∵BC=10,∠CDB=28°,
∴CD= ![]() =
= ![]() ≈21.3(米),
≈21.3(米),
答:新坡面的长为21.3米
(2)解:∵∠CAB=45°,
∴AB=CB=10,
又建筑物离原坡角顶点A处10米,即建筑物离天桥底点B的距离为20米,
当DB取最大值时,∠CDB达最小值,
要使建筑物不被拆掉DB的最大值为20﹣3=17,
则tan∠CDB= ![]() =
= ![]() ≈0.588,
≈0.588,
∴∠CDB≈31°.
答:若新坡角顶点D前留3米的人行道,要使离原坡角顶点A处10米的建筑物不拆除,新坡面的倾斜角的最小值是31°
【解析】(1)在Rt△BCD中,已知BC、∠CDB的度数,利用解直角三角形就可以求出CD的长。
(2)已知建筑物距A10米,由已知可证得△ACB是等腰直角三角形,得出AB=10,由此可求得DB的最大值,当DB取最大值时,∠CDB达最小值,然后在Rt△DBC中利用解直角三角形就可以求出∠CDB的度数。
【考点精析】本题主要考查了解直角三角形和关于坡度坡角问题的相关知识点,需要掌握解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法);坡面的铅直高度h和水平宽度l的比叫做坡度(坡比).用字母i表示,即i=h/l.把坡面与水平面的夹角记作A(叫做坡角),那么i=h/l=tanA才能正确解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
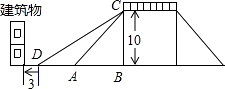
【题目】如图,△ABC的三个顶点坐标分别是A(3,3),B(1,1),C(4,-1).
(1)直接写出点A,B,C关于x轴对称的点A1,B1,C1,的坐标:A1( , ),B1( , ),C1( , ).
(2)在图中作出△ABC关于y轴对称的图象△A2B2C2.
(3)在y轴上求作一点P,使得PA+PB的值最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
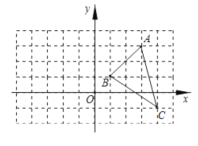
【题目】如图,D是给定△ABC边BC所在直线上一动点,E是线段AD上一点,DE=2AE,连接BE,CE,点D从B的左边开始沿着BC方向运动,则△BCE的面积变换情况是( )
A.逐渐变大
B.逐渐变小
C.先变小后变大
D.始终不变
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形![]() 的边长为
的边长为![]() ,
,![]() 为
为![]() 边上一点,
边上一点,![]() =
=![]() .
.
(1)请直接写出AE的长是________;
(2)如图(1),若![]() 为边
为边![]() 上的点,
上的点,![]() 与
与![]() 相交于点
相交于点![]() ,且
,且![]() =
=![]() .求证:
.求证:![]() ;
;
(3)如图(2),若![]() 为
为![]() 的中点,过点
的中点,过点![]() 作直线分别与
作直线分别与![]() ,
,![]() 相交于点
相交于点![]() 、
、![]() ,且
,且![]() =
=![]() .请画出示意图并求出
.请画出示意图并求出![]() 长度.
长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂设门市部专卖某产品,该每件成本每件成本30元,从开业一段时间的每天销售统计中,随机抽取一部分情况如下表所示:
销售单位(元) | 50 | 60 | 70 | 75 | 80 | 85 | … |
日销售量 | 300 | 240 | 180 | 150 | 120 | 90 | … |
假设每天定的销价是不变的,且每天销售情况均服从这种规律.
(1)秋日销售量与销售价格之间满足的函数关系式;
(2)门市部原设定两名销售员,担当销售量较大时,在每天售出量超过198件时,则必须增派一名营业员才能保证营业有序进行.设营业员每人每天工资为40元,求每件产品应定价多少元,才能使每天门市部纯利润最大?(纯利润=总销售﹣成本﹣营业员工资)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车专卖店销售A、B两种型号的新能源汽车,上周售出1辆A型车和3辆B型车,销售额为96万元;本周已售出2辆A型车和1辆B型车,销售额为62万元
(1). 求每辆A型车和B型车的售价各为多少万元?
(2). 甲公司拟向该店购买A、B两种型号的新能源汽车共8辆,购车费不少于165万元,且不超过190万元,则有哪几种购车方案?几种购车方案中所需购车费最少是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
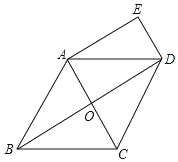
【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
(1)求证:四边形AODE是矩形;
(2)若△ABC是边长为2的正三角形,求四边形AODE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=kx+6分别与x轴、y轴交于点E,F,已知点E的坐标为(﹣8,0),点A的坐标为(﹣6,0).
(1)求k的值;
(2)若点P(x,y)是该直线上的一个动点,且在第二象限内运动,试写出△OPA的面积S关于x的函数解析式,并写出自变量x的取值范围.
(3)探究:当点P运动到什么位置时,△OPA的面积为![]() ,并说明理由.
,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com